С условиями задач можно ознакомиться здесь.
Если самое большое число из четырех единиц это 11¹¹, то для четырех двоек ответ найти несколько сложнее.
Для начала подберем все возможные комбинации:
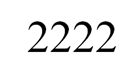
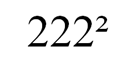
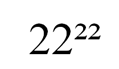
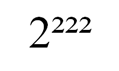

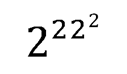

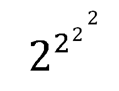
Мы получили восемь возможных комбинаций.
Очевидно, что 2222 – наименьшее из всех прочих вариантов.
Необходимо определить наибольшее число из других приведенных вариантов.
Сначала рассмотрим числа с «двухъярусным» расположением.
Сравним 222² и 22²². Для этого преобразуем 22²²:
22²² = 22²˙¹¹ = (22²)¹¹ = 484¹¹
484¹¹ больше, чем 222², так как и основание, и показатель у степени 484¹¹ больше, чем у степени 222².
Далее сравним 2²²² и 22²².
Очевидно, что 2²²² больше, чем 22²². Проведем простую проверку, заменив 22²² на гораздо большее число:
1024²² = (2¹⁰)²² = 2²²⁰
2²²² больше чем 2²²⁰
Мы нашли, что среди чисел с «двухъярусным» расположением наибольшее число: 2²²².
Сравним между собой 2²²² и оставшиеся числа:
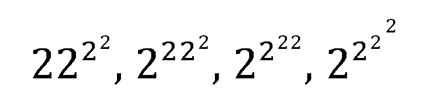
Последнее из сравниваемых число равно 2¹⁶, а потому выбывает из числа «участников соревнований».
Первое число ряда равно 22⁴, что меньше, чем 2²⁰, то есть меньше каждого из двух следующих чисел.
Нам осталось сравнить
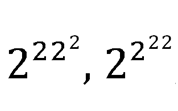
и
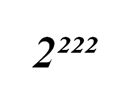
Очевидно, что больше та степень 2, показатель которой больше.
222 меньше, чем 22² = 484. Но 22² явно меньше, чем 2²².
Следовательно, наибольшее число, которое можно выразить четырьмя двойками:
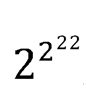
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.