С условиями задачи можно ознакомиться здесь.
Внимательно рассмотрим левую часть уравнения:
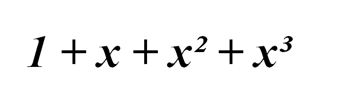
Мы можем преобразовать эту часть как
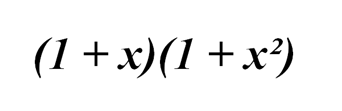
Получаем уравнение:
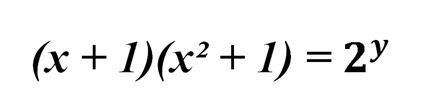
По условиям задачи, х и y – целые неотрицательные числа. В правой части у нас 2 в степени y. Это означает, что оба множителя в левой части уравнения – степени числа 2. То есть
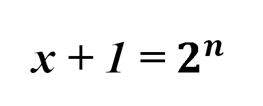
и
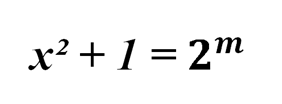
где n и m – целые неотрицательные числа.
Равенство
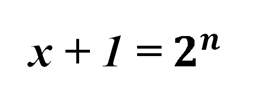
преобразуем как
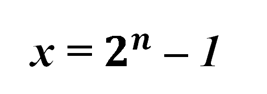
Подставим это значение х во второе равенство и получим
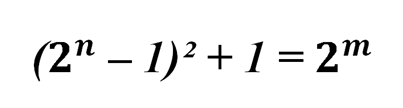
Применим формулу сокращенного умножения квадрата разности, а затем сократим обе части уравнения на 2:
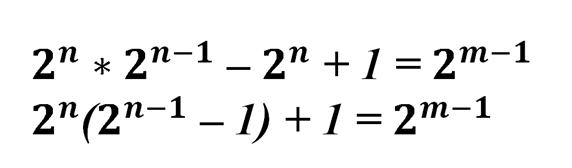
Последнее равенство невозможно при m>1, так как в этом случае справа четное число, а слева – нечетное (при n≠0) или нецелое (при n=0).
Примечание: помним, что любое число в степени 0 равно единице.
При m=0 и m=1 получаем два решения:
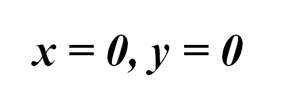
и
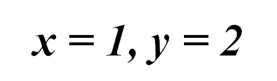
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.