Задачи №231, 232

Перед нами задача №231:
В квадрате со стороной 1 м произвольно отметили 51 точку.
Вопрос: можно ли какие-то три точки накрыть кругом радиусом 1/7 м?

Перед тем, как решать данную задачу, решим аналогичную задачу №232:
В квадрате со стороной 1 м произвольно отметили 51 точку.
Вопрос: можно ли какие-то три точки накрыть квадратом со стороной 0,2 метра?

Очевидно, что мы можем разбить квадрат со стороной 1 метр на 25 равных квадратиков со стороной 0,2 метра. Следовательно, наша задача сводится к необходимости доказать, что в каком-то квадратике находится по крайней мере 3 точки.
Для решения используем принцип Дирихле[1]. Если бы в каждом квадратике было не больше двух точек, то всего точек было бы не более 50, так как

Этот вывод противоречит условиям задачи. Значит, какой-то из квадратиков накрывает сразу три точки.

Перейдем к решению задачи №231.
Опишем вокруг квадратика со стороной 0,2 метра (см. задачу №232) окружность с диаметром, равным диагонали квадрата. Используя теорему Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов) находим квадрат длины (!) диагонали:

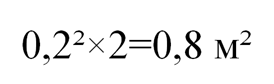
или

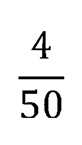
Примечание: Для решения задачи нет необходимости в точном вычислении длины диагонали.

Квадрат длины диаметра круга, который мы должны использовать по условиям задачи, равен

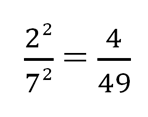
Очевидно, что квадрат длины диаметра круга, который мы собираемся использовать по условиям задачи, больше, чем квадрат длины диагонали квадратика, который, как мы уже нашли при решении задача №231, накрывает три точки. Следовательно, длина диаметра больше длины диагонали.
Это значит, какие-то три точки можно накрыть кругом радиусом 1/7 м.

[1] Иоганн Петер Густав Лежён Дирихле (13 февраля 1805 – 5 мая 1859) – немецкий математик.