Задачи №197, 198

Задача №197:
В классе 5 отличников, 20 хорошистов и 10 троечников. Отличники всегда отвечают на отлично, хорошисты могут ответить на четверку или пятерку, а троечник может ответить на тройку или, если постарается, на четверку или пятерку.
Вместо основного учителя в класс пришел подменный, который не знает никого из учеников.
Сколько человек должен в течение урока опросить учитель, чтобы наверняка была поставлена хотя бы одна пятерка?

Задача №197 решается аналогично задаче №196. То есть, для того, чтобы наверняка была поставлена хотя бы одна пятерка, необходимо в течение урока вызвать к доске 31 ученика. В противном случае, среди опрошенных учителем могут оказаться только хорошисты (20) и троечники (10), получение пятерки которыми не гарантировано.

Задача №198:
Найдите все натуральные числа n, для которых справедливы неравенства:

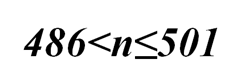
и, кроме того, верно одно и только одно из следующих условий:

1. число n четное;
2. n делится на 3;
3. n делится на 2 или на 3;
4. n не делится на 3, но делится на 4;
5. n не делится ни на 3, ни на 4;
6. n делится на 3, но не делится на 6;
7. n делится на 8 или 9;
8. n делится на 3 и на 4;
9. n делится на 11.

Пояснение: Для каждого числа n из искомого множества должно быть верно только одно из этих девяти условий.

Для решения этой необходимо внимательно изучить все предложенные условия, обращая внимание на то, что должно быть «верно одно и только одно» из предложенных условий.

Если выполнено условие 1) или условие 2), то условие 3) также выполнено. Одновременное выполнение условий 1) и 3) или 2) и 3) противоречит установленным в задаче требованиям. Это означает, что условия 1), 2), 3) не выполнены.

Условие 4) приводит нас к четному числу (см. условие 1)). Значит, и условие 4) не выполнено.

Не выполняются и условия 6), 7), 8) (сравните с условиями 1), 2), 3) ).

Анализ условий приводит к тому, что выполнено условие 5), а в отношении условия 9) можно сказать, что при его выполнении может быть выполнено и условие 5). Значит, условие 9) не выполнено. Примечание: мы последовательно убираем условия, которые не могут быть выполнены не для конкретного диапазона чисел, а по требованиям задачи.

Из представленного нам диапазона необходимо выбрать натуральные числа n, которые не делятся ни на 2, ни на 3, ни на 11. Числа, отвечающие требованиям задачи: 487, 491, 493, 497, 499.