Задачи №193, 194, 195, 196, 197, 198

Перед нами стояла задача (задача №193): Предоставьте козе для выпаса сектор, используя не более пяти колышков.

Способ решения такого рода задач разобран в теме Коза на привязи и Коза на привязи_2.

Для «выделения козе» сектора с углом, меньше развернутого, необходимо построить пересечение параллелограмма и круга.
Как построить параллелограмм с помощью четырех колышков мы разбирали при решении задачи №189. Круг – это еще один колышек с привязью. Итого мы затратим пять колышков.
В случае необходимости развернутого решения (построения схемы), напишите об этом в комментариях.

Перейдем к задачам, решение которых построено на отрицании предложенных утверждений.
Примечание: Важно понимать, что мы не определяем «вероятность события», указанного в утверждении, а отвечаем на вопрос, поставленный в задаче. При этом мы строим свое решение на возможности (именно возможности, а не вероятности) иного исхода.

Задача №194
Известно, что в урне не все шары белые. Верно ли, что там есть красный шар?

Задача очень простая. Утверждение, данное в ней неверно, так как может оказаться, что помимо белых шаров все остальные черные или, например, зеленые.

Задача №195
Известно, что в урне не все шары одного цвета. Верно ли, что в урне есть хотя бы один цветной шар?

Исходя из того, что в урне шары как минимум двух цветов, мы можем уверенно сказать, что утверждение, данное в задаче, верное.

Задача №196
В урне 10 белых, 8 синих, 11 зеленых шаров. Сколько надо вынуть шаров, чтобы наверняка:

• попался белый шар,
• попались шары всех трех цветов?

Если вынуть 19 шаров, то они могут оказаться только синими и зелеными. Это значит, что для того, чтобы наверняка попался белый шар, необходимо вынуть 20 шаров.
Аналогично отвечаем на второй вопрос задачи. Если вынуть 21 шар, то может оказаться, что мы вынули все белые и зеленые шары, но не вынули синий. Значит, необходимо вынуть 22 шара.

К задачам, решение которых построено на отрицании, относится, кстати, и задача №161 «Кто же лидер?».

Попробуйте с помощью построения отрицания решить следующие задачи.

Задача №197:
В классе 5 отличников, 20 хорошистов и 10 троечников. Отличники всегда отвечают на отлично, хорошисты могут ответить на четверку или пятерку, а троечник может ответить на тройку или, если постарается, на четверку или пятерку.
Вместо основного учителя в класс пришел подменный, который не знает никого из учеников.
Сколько человек должен в течение урока опросить учитель, чтобы наверняка была поставлена хотя бы одна пятерка?

Задача №198:
Найдите все натуральные числа n, для которых справедливы неравенства:

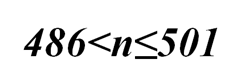
и, кроме того, верно одно и только одно из следующих условий:

1. число n четное;
2. n делится на 3;
3. n делится на 2 или на 3;
4. n не делится на 3, но делится на 4;
5. n не делится ни на 3, ни на 4;
6. n делится на 3, но не делится на 6;
7. n делится на 8 или 9;
8. n делится на 3 и на 4;
9. n делится на 11.

Пояснение: Для каждого числа n из искомого множества должно быть верно только одно из этих девяти условий.

Решение задач №197, 198 не позднее, чем 16.04.2024.