Задачи №204, 205

Решим задачу №204:
Среди множества чисел, которое описано в задаче №203, сколько существует таких, в записи которых цифры не повторяются?

Напомню условия задачи №203:
Сколько существует различных вариантов трехзначных чисел, в которых участвуют только цифры 1, 2, 3, 4?

Для решения этой задачи снова представим себе стеллажи с ящиками (см. задачу №203).
Согласно условиям задачи, цифры в числах не должны повторяться.
Значит, в стеллаже №1 мы уберем первый ряд ящиков: 111, 112, 113, 114.
В стеллаже №2 мы убираем второй ряд ящиков: 221, 222, 223, 224.
Аналогичную операцию проводим с третьим рядом стеллажа №3 и четвертым рядом стеллажа №4.
Количество комбинаций (ящиков), которые у нас остаются:

4 стеллажа * 3 ряда в каждом * 4 ящика в ряду = 48 комбинаций

Но есть ящики, чьи номера содержат совпадения третьей цифры с первой или второй. В каждом из рядов это два ящика. Например, 121 и 122, 131 и 133, 141 и 144.
То есть мы убираем еще шесть ящиков из каждого нашего стеллажа.
Остается:

4 стеллажа * 3 ряда в каждом * 2 ящика в ряду = 24 комбинации.

Значит, у нас всего 24 возможных комбинации, числе, удовлетворяющих нашим условиям.

Разберем второй вариант решения.

В качестве первой цифры числа, которое мы должны «построить», может выступать цифра 1, 2, 3 или 4. То есть, возможны 4 варианта выбора первой цифры.
Вторая цифра искомого числа не должна повторять первую. Это означает, что для выбора второго числа число вариантов уменьшается на один. У нас будет только 3 возможных варианты выбора второй цифры.
Третья цифры не должна совпадать с первой и второй цифрой. Значит, для выбора третьей цифры остается только 2 возможных варианта.

Мы получаем количество возможных вариантов:

4 для первой цифры * 3 для второй цифры * 2 для третьей цифры = 24 возможных комбинации.

Схематично это можно изобразить так (рисунок 1):

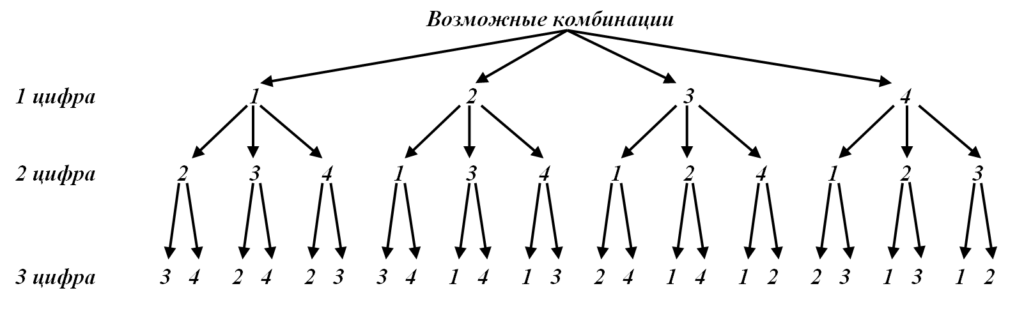
Мы использовали правило перемножения возможностей.

Используя это правило, решите следующую задачу (задача №205):
Две группы туристов находятся в двух разных лагерях в зоне видимости друг друга, но сотовая связь, интернет, радиосвязь, спутниковая связь отсутствует.
Туристы договорились, что для передачи сообщений будут использовать кодировку из флажков. Для этого в каждой группе есть пять флажков разного цвета: красный, зеленый, белый, черный, синий.
Для передачи сообщения на мачте вывешивается только три флажка, один под другим.
При этом значение имеет и цвет флажка, и порядок, в котором он вывешивается. То есть, если сверху черный, затем белый, потом зеленый, то это одно сообщение. А если вывешивается сверху зеленый, затем черный, а в самом низу белый – то это другое сообщение.
Одна комбинация соответствует одному оговоренному сообщению.
Сколько различных сообщений можно закодировать таким образом?

Решение задачи №205 здесь: Задачи №205, 206.