Задачи №201, 202, 203, 204

Решим задачу (задача №201):
Вам необходимо выяснить у вашего собеседника некий номер, состоящий из пяти цифр.
Вы можете задавать вопросы вашему собеседнику, на которые он отвечает «да» или «Нет».
Какой способ вы должны выбрать, чтобы количество вопросов было минимальным? И сколько минимально вам потребуется вопросов?

Решение аналогичных по смыслу задач мы рассматривали здесь: Математика и программирование. Логика поиска.

Для решения нашей задачи необходимо определить количество возможных вариантов. В нашем случае количество возможных вариантов – 10⁵. Определению количества возможных вариантов чисел, состоящих из пяти произвольных цифр, посвящен раздел математики – комбинаторика.
К комбинаторике мы вернемся позже, а сейчас нам необходимо найти минимальное количество вопросов для выяснения загаданного номера.
Мы должны действовать по принципу, который использовали в задачах 199, 200, то есть каждый вопрос должен приводить к уменьшению количества возможных вариантов.
Так как собеседник будет отвечать на наш вопрос только «Да» или «Нет», то количество возможных вариантов должно уменьшаться вдвое после каждого ответа. Всего вариантов, как мы уже указали, 10⁵, то есть 100000.
Начнем с вопроса: «Загаданный номер больше 50000?». Ответ приведет нас к той половине возможного множества вариантов, которая будет содержать искомый номер. Допустим, нам ответили «Нет». Тогда следующий вопрос: «Загаданный номер больше 25000?». Спросить «больше» или «меньше» значения не имеет, так как полученный ответ в любом случае позволит выбрать необходимую часть множества.

Сколько же всего вопросов необходимо задать?

Каждый вопрос уменьшает множество вариантов в два раза. Или, если выразиться иначе, у нас имеется два в степени n возможных вариантов.

То есть 16 вопросов может не хватить для поиска, но 17 вполне достаточно. Значит, количество необходимых вопросов: 17.

Попробуйте решить аналогичную задачу, но с условием, что собеседник на один из вопросов может дать неправильный ответ (задача №202). Как изменятся ваши вопросы? Какое наименьшее количество вопросов необходимо будет задать для поиска задуманного номера?

Вернемся к комбинаторике.

Комбинаторика — раздел математики, посвящённый решению задач, связанных с выбором и расположением элементов множества в соответствии с заданными правилами. Задаваемое правило определяет выборку из элементов исходного множества, которая называется комбинаторной конфигурацией.

Решим, например такую задачу (задача №203):
Сколько существует различных вариантов трехзначных чисел, в которых участвуют только цифры 1, 2, 3, 4?

Если мы начнем выписывать все возможные варианты, то потратим довольно много времени. Представьте, что вам необходимо найти все возможные варианты девятизначного числа? Или, например, все возможные варианты с цифрами 1, 2, 3, 4, 5, 6.
Перебирать все возможные варианты, а потом их подсчитывать – удовольствие очень сомнительное. Поэтому нам необходим иной способ.

Представьте себе четыре архивных стеллажа.
В каждом стеллаже по четыре ряда ящиков. В каждом ряду по 4 ящика. Все ящики пронумерованы.
Первый стеллаж содержит комбинации с цифрой 1.
Пронумеруем первый ряд. Номер начинается как цифра номера стеллажа, затем цифра номера ряда, а далее – цифра порядкового номера ящика:

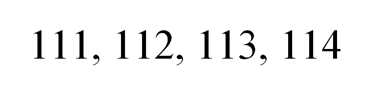
По аналогии второй ряд будет пронумерован так:

Не трудно догадаться, что четвертый ряд ящиков четвертого стеллажа будет пронумерован следующим образом:

Количество ящиков во всех четырех стеллажах можно легко найти:

4 стеллажа * 4 ряда ящиков в каждом стеллаже * 4 ящика в ряду.

Это и есть возможное количество комбинаций для нашей задачи:

Количество комбинаций: четыре возможных цифры для всевозможных вариантов из трех цифр заданного ряда: 1, 2, 3, 4.

Искомое количество вариантов: 64.

При решении задачи №201 мы определяли возможное количество вариантов для числа из пяти произвольных цифр. Так как цифры для искомого числа находятся в диапазоне от 0 до 9 (то есть 10 возможных цифр для выбора), а количество цифр в искомом номере – пять, то количество вариантов в задаче №201 составило 10⁵.

Мы разобрали довольно простой вариант.

Попробуйте решить задачу №204:
Среди множества чисел, которое описано в задаче №203, сколько существует таких, в записи которых цифры не повторяются?

Ответ к задаче №204 здесь: Комбинаторика_2