Задача №206

Необходимо решить следующую задачу (задача №206):
Сколько существует способов выбрать из группы лиц, численностью N человек:

• троих на три должности;
• пятерых на пять должностей;
• M лиц на M должностей, при M ≤N?

Логика поиска ответа на первый вопрос задачи такая же, как и для решения задач №204 и №205.

На первую должность мы выбираем из N человек, имея N возможностей для выбора.
На вторую должность мы будем выбирать из (N – 1) человек. Значит, у нас (N – 1) возможностей.
Соответственно, для выбора на третью должность у нас будет (N – 2) возможностей.
Итоговое число возможностей для выбора:

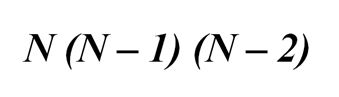
Следовательно, для ответа на второй вопрос задачи, необходимо продолжить логическую цепочку уменьшения количества возможностей:
(N – 3) для четвертой должности,
(N – 4) для четвертой должности.

Итоговое число возможностей для выбора:

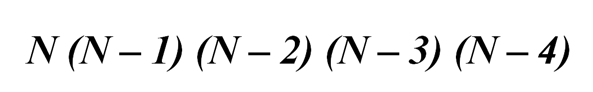
Продолжение логической цепочки приводит нас к ответу на третий вопрос задачи. Мы получаем число способов для выбора M лиц на M должностей, при M ≤N, равное произведению M последовательных натуральных чисел, наибольшее из которых равно N:

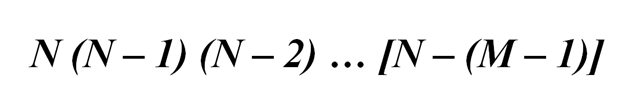
В общем случае полученное решение можно изложить так: число размещений n элементов по m равно произведению m последовательных натуральных чисел, наибольшее из которых n.
Число размещений n элементов по m обозначается как

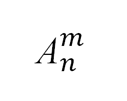
Здесь А – первая буква французского слова Arrangement.