В «События и вероятности_4» мы разбирали решение задачи №215:
Представьте, что проводится турнир по олимпийской системе (плей-офф). Допустим, это греко-римская борьба.
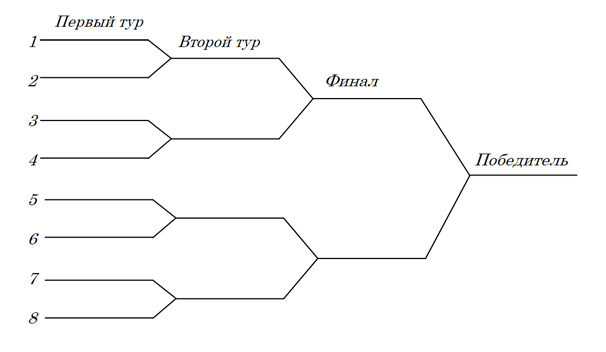
Номер участника определяет его положение в турнирной таблице (рис. 1), но не привязан к мастерству участника соревнований.
Предположим, что есть некий лучший по мастерству участник, который всегда побеждает остальных участников соревнований.
Есть так же второй по мастерству участник, который также всегда побеждает остальных участников соревнований, за исключением лучшего участника, которому он проигрывает.
Исходя из системы (см. рисунок 1), второе место займет тот участник, который проиграет в финале.
Какова вероятность того, что второе место займет второй по мастерству участник?

Попробуем решить задачу №216:
Допустим, что проводится рыцарский турнир в порядке, аналогичном тому, который описан в задаче №215. Порядок состязаний определяется жребием.
Нам неизвестно мастерство участников, но в турнире принимают участие два близнеца.
Какова вероятность того, что они встретятся в поединке?

Для удобства обозначим близнецов через А и Б.
После того, как А занимает одно из мест в таблице, для Б равновозможны 7 оставшихся вариантов. Тогда вероятность, что близнецы попадут в одну пару в первом туре, равна ¹∕₇.

Вероятность того, что Б окажется в соседней паре равна ²∕₇ (Б может оказаться вместе с А в «верхней» половине таблицы, но в другой паре, а также вместе с А в «нижней» половине таблицы, но в разных парах). В этом случае А и Б встретятся во втором туре, при условии, что выиграют первый тур. Вероятность этого события (выигрыша) равна ¼.
Следовательно, вероятность того, что близнецы встретятся во втором туре, равна:

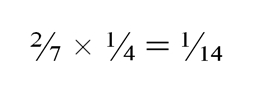
Остается случай, когда близнецы находятся в разных половинах турнирной таблицы. Вероятность того, что Б окажется в другой половине турнирной таблицы равна ⁴∕₇. Вероятность того, что близнецы выиграют проводимые состязания с другими противниками для прохождения в финал, будет равна:

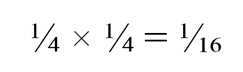
Значит, вероятность встречи близнецов в финале равна:

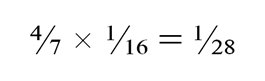
Остается сложить вероятности встречи в первом, втором и третьем туре (финале):

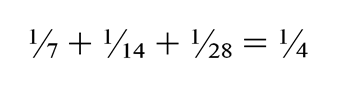
Вероятность того, что близнецы встретятся в поединке, равна ¼.