Задачи №213, 214, 215, 216

Рассмотрим решение задачи, предложенной Антуаном Гомбо[1] Блезу Паскалю^[2] (задача №213):
Одновременно бросают три игральных кости (кубики с нанесенными на грани числами от 1 до 6).
Что вероятнее: что сумма очков на верхних гранях равна 11 или то, что эта сумма равна 12?
Каковы вероятности этих событий?

Решение, предложенное Гомбо, привело его к заключению, что сумма очков 11 может встретиться с той же частотой, что и сумма очков 12 (см. «Задача шевалье де Мере»). Но это заключение не нашло подтверждения при проведении игр (испытаний).
Блез Паскаль, как уже говорили, решил эту задачу иначе, опровергнув рассуждения Гомбо.
В чем же заключалась ошибка Гомбо? Она заключалась в неправильном подсчете возможных исходов выпадения кубиков.

Допустим, комбинация выпадения на трех кубиках очков на общую сумму, равную 12 при числах 4+4+4, только одна. Но комбинаций 1+5+6 может быть несколько:

Найдем вероятность того, что сумма очков на верхних гранях трех игральных костей равна 11, и того, что эта сумма равна 12. Для начала вычислим количество равновозможных исходов (см. Комбинаторика):

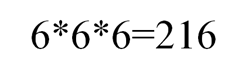
У нас 216 равновозможных исходов различных комбинаций чисел на верхних гранях кубиков (костей).
Получить на верхних гранях сумму очков, равную 11, если переформулировать варианты, уже рассмотренные Гомбо, можно шестью способами:

• Выпали числа 1, 4, 6;
• Выпали числа 1, 5, 5;
• Выпали числа 2, 3, 6

и т.д. (см. «Задача шевалье де Мере»).

Необходимо подсчитать количество благоприятных исходов для каждого способа.
Для удобства обозначим комбинации (исходы) как последовательное указание чисел на верхних гранях кубиков. Например, выпадение числа 1 на первом кубике, числа 4 на втором кубике, числа 6 на третьем кубике, обозначим как 146.
Для способа 1, 4, 6 возможны исходы: 146, 164, 416, 461, 614, 641. Итого шесть возможных исходов.
Для суммы очков, равной 11, как уже было указано выше, возможны способы:

Несложно подсчитать количество возможных исходов для каждого способа, исходя из количества вариантов чисел и возможных вариантов комбинаций выпадения. Как мы уже посчитали для способа 1, 4, 6, у нас шесть исходов, исходя из того, что каждое из трех чисел может давать по две комбинации с оставшимися числами.

Значит для способа 1, 5, 5 у нас три исхода, для способа 2, 3, 6 – шесть исходов, и т.д. Продолжив логическую цепочку, мы получим, что для получения на верхних гранях суммы очков, равной 11, благоприятны 27 исходов:

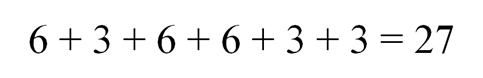
Аналогично можно посчитать количество благоприятных исходов для получения на верхних гранях суммы очков, равной 12:

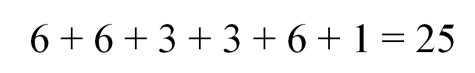
Все шесть способов получения суммы очков 12 указаны здесь: «Задача шевалье де Мере». Исходя из этих способов, мы и посчитали количество исходов.

Осталось рассчитать вероятность того, что сумма очков на верхних гранях равна 11 и того, что эта сумма равна 12:

Гомбо оказался неправ. Вероятность выпадения кубиков с суммой очков, равной 11 выше, чем с суммой очков, равной 12.

Решим задачу №214
Какова вероятность того, что наудачу выбранное четырехзначное число составлено только из нечетных цифр?

Всего у нас 9000 четырехзначных чисел, расположенных в ряду от 1000 до 9999.
Нечетных цифр всего 5.
На месте тысяч может стоять любая из пяти нечетных цифр. Равно как и на месте сотен, десятков, единиц может стоять любая из нечетных цифр.
Это означает, что вариантов составления четырехзначных чисел, составленных только из нечетных цифр:
5*5*5*5 = 625
Исходя из условий задачи, равновозможен любой вариант выбора числа из 9000.
Значит, вероятность того, что наудачу выбранное четырехзначное число составлено только из нечетных цифр, равна:

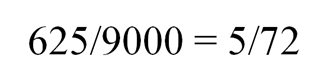
Решим задачу №215
Представьте, что проводится турнир по олимпийской системе (плей-офф). Допустим, это греко-римская борьба.
Номер участника определяет его положение в турнирной таблице (рис. 1), но не привязан к мастерству участника соревнований.
Предположим, что есть некий лучший по мастерству участник, который всегда побеждает остальных участников соревнований.
Есть так же второй по мастерству участник, который также всегда побеждает остальных участников соревнований, за исключением лучшего участника, которому он проигрывает.
Исходя из системы (см. рисунок 1), второе место займет тот участник, который проиграет в финале.
Какова вероятность того, что второе место займет второй по мастерству участник?

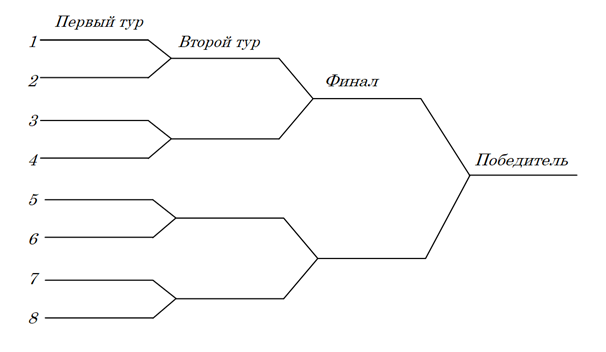
Вполне очевидно, что второй по мастерству участник может занять второе место в финале только тогда, когда он находится в той половине турнирной таблицы, в которой нет лучшего участника. В противном случае он проиграет лучшему участнику не успев дойти до финала.
В турнирной таблице второй участник может занять любую из семи ступеней (начальных мест), не занятых лучшим участником. Значит, имеется семь равновозможных исходов.
Но благоприятны для второго по мастерству участника (приведут в финал) только четыре ступени.
Значит, искомая вероятность равна:
4/7

Попробуйте решить задачу №216:
Допустим, что проводится рыцарский турнир в порядке, аналогичном тому, который описан в задаче №215. Первоначальное место в турнирной таблице определяется жребием.
Нам неизвестно мастерство участников, но в турнире принимают участие два близнеца.
Какова вероятность того, что они встретятся в поединке?

Ответ к задаче №216 здесь: События и вероятности. Близнецы

---

[1]     Гомбо́ Антуа́н (1607 – 29 декабря 1684) – французский писатель, известный также, как шевалье де Мере́, по имени персонажа его книг.

[2]    Паска́ль Блез (19 июня 1623 – 19 августа 1662) – французский математик. Механик, физик, литератор, философ, теолог.