Задачи №229, 230

Используя принцип Дирихле, решим задачу №229:
В доме 123 жильца. Всем жильцам вместе 3813 лет.
Можно ли среди всех жильцов дома выбрать сотню, которым вместе будет не меньше 3 100 лет?

Расположим жильцов по возрасту и «возьмем» сто самых старших. Возраст самого молодого жильца из «старшей сотни» не меньше, чем возраст тех, кого не включили в список этой «старшей сотни».
Предположим, что сумма возрастов отобранной сотни менее 3 100 лет. Тогда возраст самого молодого из них менее

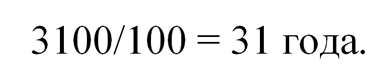
Следовательно, возраст каждого из не вошедшего в «сотню старших» тоже меньше 31 года.
Это означает, что сумма возрастов тех, кто не вошел в «сотню», меньше чем

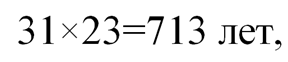
а сумма возрастов всех жильцов меньше чем

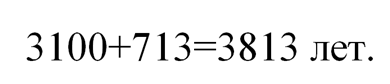
Этот вывод противоречит условиям задачи.

Необходимо отметить, что сумма возрастов «старейшин» равна 3100 лет тогда и только тогда, когда все жильцы имеют один и тот же возраст – 31 год.

Вопрос на внимательность: Почему возраст самого молодого жильца из «старшей сотни» не меньше, чем возраст тех, кого не включили в список этой «старшей сотни»?

Для ответа на этот вопрос решите задачу №230:
Правда ли, что если у любого воображаемого дерева оборвать 8/15 его листьев (чисто теоретически), то останется не менее 7/15 тени (по площади), которую давало воображаемое дерево.
Дополнительные условия:

• Тенью от ствола и веток пренебречь;
• Число листьев считать делящимся на 15.

Решение к задаче №230 здесь: И снова принцип Дирихле_2