Задачи №230, 231

Используя принцип Дирихле, решим задачу №230:
Правда ли, что если у любого воображаемого дерева оборвать 8/15 его листьев (чисто теоретически), то останется не менее 7/15 тени (по площади), которую давало воображаемое дерево.
Дополнительные условия:

• Тенью от ствола и веток пренебречь;
• Число листьев считать делящимся на 15.

Для решения этой задачи потребуется сильное воображение.
Первоначально расположим мысленно листья по величине отбрасываемой ими тени. Понимаем, что тени частично перекрываются! Действуя таким образом, присвоим листьям номера, начиная от первого листа, которому поставим в соответствие всю его тень, какую отбрасывал бы он, если бы был один на дереве. Всего у нас m листьев.

Второму листу поставим в соответствие множество, являющееся разницей между его собственной тенью и тенью, отнесенной к первому листу.
Нумеруя листья таким образом, мы дойдем до листа n, которому поставим в соответствие разность между его собственной тенью (если бы он был один) и объединением теней листов 1, 2, 3,  … , (n – 1).

Возможно, что некоторым листьям будет поставлено в соответствие пустое множество (площадь тени равна нулю).
Упорядочить листья следует по величине площади тени, приписываемой каждому листу.
Условно «оборвем» 8/15 листьев, начиная с наименьшего по тени конца нашей цепочки.
Оставшиеся 7/15 листьев дают не менее 7/15 тени.
Для доказательства этого утверждения предположим противное: все оставшиеся листья дают менее 7/15 тени.
Последний оторванный лист, соответственно, дает менее 7/15:7/15m тени, где m – число листьев (см. выше).

Если оборванные листья дают не больше тени, чем последний из необорванных, то все оборванные листья вместе занимают менее 8/15 тени.
Это означает, что все листья вместе отбрасывают менее

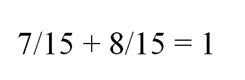
всей тени, что противоречит условию задачи.

Еще одна задача, решить которую поможет использование принципа Дирихле (задача №231):
В квадрате со стороной 1 м произвольно отметили  51 точку.
Вопрос: можно ли какие-то три точки накрыть кругом радиусом 1/7 м?

Решение к задаче №231 здесь: Геометрия и принцип Дирихле