Задачи №235, 236, 237

Представляю вам на выбор несколько задач.

Задача №235:
Представьте себе бесконечную шахматную доску. На полях (в ячейках) этой доски записаны натуральные числа так, что каждое число равно среднему арифметическому четырех соседних чисел – верхнего, нижнего правого и левого.
Сможем ли мы доказать, что все эти числа равны между собой?

Задача №236:
На прямой задано множество точек М. Каждая точка из М является серединой отрезка, соединяющего две другие точки из М.
Необходимо доказать, что множество М бесконечно.

Задача №237:
На плоскости задано некоторое множество точек М. Каждая точка из М является серединой отрезка, соединяющего какую-либо пару точек того же множества М.
Необходимо доказать, что множество М бесконечно.

Перед тем, как решить предложенные задачи, рассмотрим подход к решению данных задач, который носит название – правило «крайнего». Он означает, что для решения необходимо рассмотреть объект, обладающий «крайними», или, иными словами, экстремальными свойствами. Например, при рассмотрении некого набора чисел правило (принцип) «крайнего» может применяться при рассмотрении через рассмотрение наибольшего или наименьшего из этих чисел.

Начнем с решения задачи №236.
Пойдем от противного и предположим, что множество М конечное.
В таком случае, среди его точек есть крайние точки – самая правая и самая левая. Если таковые точки существуют, что обозначим одну из них буквой А. Например, крайнюю левую. Точка А не может лежать внутри отрезка, соединяющего две другие точки множества точек М, так как она, исходя из логики нашего утверждения, крайняя.
Но условия задачи таковы, что каждая точка из М является серединой отрезка, соединяющего какую-либо пару точек того же множества М. Это означает, что точка А не принадлежит множеству М.
Используя некую «крайнюю» точку А мы получили противоречие условиям задачи.

Задача №236 имеет и еще одно решение, также основанное на правиле «крайнего».
Мы вновь пойдем от противного, допуская, что множество М конечное, но рассматривать будем длины отрезков, соединяющих точки множества М. Набор чисел, которыми можно выразить длину, конечен. Для рассмотрения выберем некий отрезок от точки В до точки С, принадлежащих множеству М. Предположим, что крайний по величине, но в сторону наибольшего.
Вне отрезка ВС не может быть точек из М, иначе придется признать, что существует отрезок с большей, чем у отрезка ВС длиной. Значит, все точки множества М лежат на отрезке ВС. Тогда точки В и С не удовлетворяют условию задачи, указывающему, что каждая точка из М является серединой отрезка, соединяющего какую-либо пару точек того же множества М. То есть точки В и С не принадлежит множеству М.

Мы вновь получили противоречие.
Таким образом, множество М бесконечно.

Условия решенной задачи не предполагали наличие каких-либо «крайних» вариантов. Но, искусственно задав условные рамки предложенному в задаче множеству, мы исследовали возможные «крайние» случаи (предельные величины) заданных границ (рамок), противоречащих условиям задачи. Доказывая «от противного» и используя правило «крайнего», мы пришли к решению задачи.

Решим задачу №237:
На плоскости задано некоторое множество точек М. Каждая точка из М является серединой отрезка, соединяющего какую-либо пару точек того же множества М.
Необходимо доказать, что множество М бесконечно.

Поступим аналогично тому, как мы поступали при решении задачи №236, то есть, предположим, что множество М конечно.
Применим правило «крайнего», предположив, что есть некая самая крайняя левая нижняя точка множества М (можно рассматривать самую крайнюю правую верхнюю точку или, например, самую крайнюю правую нижнюю точку).
Обозначим эту точку буквой А.
Точка А не может лежать внутри отрезка, соединяющего две точки множества М, так как, если бы такой отрезок существовал, то один из его концов находился бы левее А, либо на одной с А вертикали, но ниже. Любой из вышеописанных вариантов невозможен в силу выбора условий нахождения точки А (см. выше).

В задаче №236 мы также рассмотрели вариант доказательства через попарное расстояние между точками множества М.
Рассмотрим аналогичное решение для задачи №237.
Если множество М конечно (идем, напомню, от противного), то и попарных расстояний конечное число. Среди них, руководствуясь применяемым нами правилом «крайнего», можно отыскать наибольшее.
Возьмем некие точки А и В, относящиеся к множеству М и находящиеся на наибольшем расстоянии друг от друга. Иными словами, расстояние между любыми точками из М не превосходит длину отрезка АВ.
Должен быть некий отрезок СЕ, серединой которого является точка В (см. условия задачи).
Точки С и Е не могут лежать на прямой АВ, иначе одна из указанных точек оказалась бы удалена от А на расстояние большее, чем длина отрезка АВ. Тогда, точки А, С, Е являются вершинами треугольника, в котором АВ является медианой.
Медиана, проведенная к одной из вершин треугольника, всегда меньше полусуммы двух других сторон. Это означает, что она (медиана) меньше хотя бы одной из этих двух сторон треугольника. Рассмотрите, например, параллелограмм АСКЕ, построенный на сторонах АС и АЕ треугольника САЕ (рис. 1).

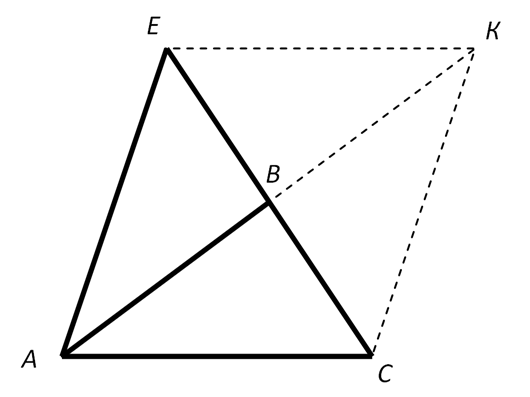
В описанном параллелограмме длина АК равна удвоенной длине АВ, но меньше сумм длин двух сторон (АС + СК или АЕ + ЕК, АС + АЕ).
Следовательно, длина АВ не может являться наибольшей из попарных расстояний. Мы вновь получили противоречие.

Попробуйте решить задачу №235 самостоятельно. Решение задачи №235 можно посмотреть здесь: Правило (принцип) «крайнего»_2.