Задачи №235, 238

Решим задачу №235:
Представьте себе бесконечную шахматную доску. На полях (в ячейках) этой доски записаны натуральные числа так, что каждое число равно среднему арифметическому четырех соседних чисел – верхнего, нижнего правого и левого.
Сможем ли мы доказать, что все эти числа равны между собой?

Для решения воспользуемся правилом «крайнего» (см. Правило (принцип) «крайнего»). В качестве «крайнего» используем наименьшее натуральное число. Такое число обязательно должно существовать среди чисел, записанных на полях нашей шахматной доски.
Для того, чтобы в этом убедиться, предположим, что К – одно из данных в задаче чисел.
Если на одном из полей доски записана единица, то она и есть наименьшее натуральное число. Если же единицы на полях нашей доски нет, то двойка и будет наименьшим натуральным числом для нашего случая.
В случае, если нет двойки, то мы обратимся к поискам тройки и т.д.
Нам потребуется не более чем К шагов, для поиска наименьшего натурального числа, которое записано на полях нашей доски.

Мы, собственно, имеем дело с принципом наименьшего числа (элемента), который гласит следующее: «всякое непустое подмножество множества натуральных чисел содержит наименьшее число». В любом непустом множестве натуральных чисел есть наименьшее. В пустом множестве нет ни одного элемента, так что для него принцип наименьшего числа нарушается.

Обозначим наименьшее из чисел, записанных на нашей доске, буквой m.
Рассмотрим условное поле P, на котором это число записано. Числа, записанные на соседних полях, обозначим буквами a, b, c, d.

Смотрим условия задачи:

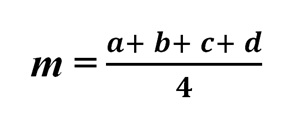
Отсюда,

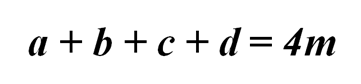
Мы выбрали m, как наименьшее число. Значит,

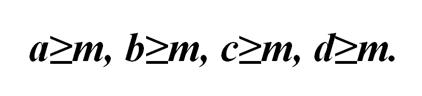
Предположим, что хотя бы одно из этих неравенств строгое. Тогда

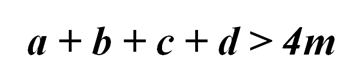
Следовательно,

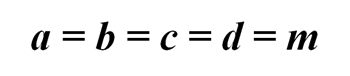
То есть, соседние числа равны m.

Вывод, который мы можем сделать: если на некотором поле нашей шахматной доски записано число m, то и на соседних полях записано число m.
Отсюда можно сделать и обобщающий вывод: на горизонтали, содержащей поле P, записаны только числа m, а, следовательно, и на любой вертикали записано число m, так как вертикали пересекают горизонталь с числами m.
Это означает, что вообще все числа на нашей шахматной доске равны m, то есть равны между собой.

Попробуйте решить задачу №238:
На квадратной шахматной доске размером n×n клеток расставлены ладьи (тура, башня). Условие, которому соответствует расстановка: если некоторое поле свободно, то общее количество ладей, стоящих на одной с этим полем горизонтали или на одной с ним вертикали, не менее n.
Необходимо доказать, что на доске имеется не менее чем следующее количество ладей:

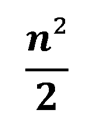
Решение задачи №238 можно посмотреть здесь: Правило (принцип) «крайнего»_3.