Задачи №240, 241

Решим задачу №240:
На плоскости заданы n точек. Никакие три из заданных точек не лежат на одной прямой.
Необходимо доказать, что существует окружность, проходящая через три из данных точек, но не содержащая внутри ни одной из данных точек.

Представьте, что вы провели окружности через каждую тройку точек, получив при этом некоторое количество окружностей. Допустимо, что некоторые окружности могут слиться в одну. Утверждение, которое необходимо доказать, будет верно, если хотя бы одна из этих окружностей не содержит внутри себя ни одной из данных точек.
Если предположить, что рассмотрение наименьшей окружности приведет нас к верному ответу, то мы, следуя такому предположению, окажемся на ложном пути, так как вполне может быть конфигурация из неких пяти точек, составляющая собой квадрат (четыре точки) и его центр (пятая точка). Наименьшей окажется окружность, описанная около квадрата, но в центре такой окружности будет находиться точка, что противоречит условиям задачи.

Первоначально решим «вспомогательную» задачу, а именно найдем окружность, проходящую через две из данных точек, не содержащую внутри ни одной из данных точек.
Здесь мы можем воспользоваться правилом крайнего и выбрать пару точек А и В, находящихся на наименьшем расстоянии друг от друга. Так как мы выбрали точки, находящиеся друг от друга на наименьшем расстоянии, то остальные (n – 2) точки находятся за пределами окружности с диметром АВ, так как удалены от А и В не менее, чем на АВ.

Можем переходить к решению исходной задачи.
Мы провели окружность через найденные точки А и В. Представим, что мы проводим окружности через А и В, а также через каждую из оставшихся (n – 2) точек. Одна из таких окружностей окажется наименьшей. Предположим, что это окружность, проходящая через точки А, В, С.
Необходимо доказать, что эта окружность удовлетворяет условиям задачи и не содержит внутри других точек.
АС ≥ АВ и ВС ≥ АВ. Это означает, что угол С в треугольнике АСВ острый.
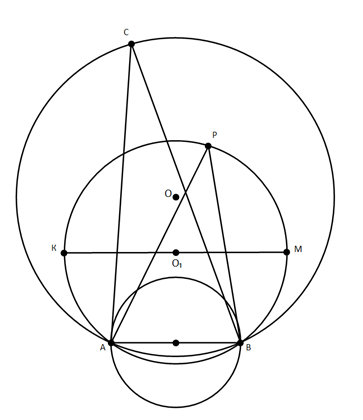
Предположим, что внутри окружности АСВ есть некая из данных точка Р (см. рис. 1).
Угол Р в треугольнике АРВ острый, аналогично углу С в треугольнике АСВ. Это означает, что центры О окружности АСВ и О₁ окружности АРВ расположены по одну сторону общей хорды АВ.
Дуга АРВ находится внутри окружности АСВ. Проведем диаметр КМ окружности АРВ параллельно хорде АВ. Указанный диаметр лежит внутри окружности АСВ. Это означает, что окружность АРВ меньше окружности АСВ и, соответственно, окружность АРВ меньше окружности АСВ, что противоречит сделанному нами выбору окружности АСВ, как наименьшей.

Мы получили доказательство утверждения, данного в задаче.

Решите задачу №241:
Верно ли утверждение, что не существует четверки натуральных чисел: x, y, z, u, удовлетворяющих уравнению

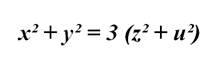
Решение задачи №241 можно посмотреть здесь: Правило (принцип) «крайнего»_6