Задачи №242, 243

Реши, используя правило «крайнего», задачу №242:
На плоскости расположено n прямых. При этом n≥3.
Любые две прямые пересекаются и через каждую точку пересечения проходит не менее трех из данных прямых.
Необходимо доказать, что все прямые пересекаются в одной точке.

Обозначим точку пересечения прямых буквой М. Предположим, пойдя способом «от противного», что М – не единственная точка пересечения прямых. Исходя из такой постановки вопроса, найдется прямая данной системы (обозначим её – l₁), которая не проходит через М.
Множество точек пересечения, не лежащих на l₁, не пусто. В это множество входит, например, вышеуказанная точка М.
Рассмотрим точку множества точек пересечения, не лежащих на l₁, ближайшую к l₁. Если таковых точек несколько, то есть имеется несколько точек, находящихся на минимальном расстоянии от l₁, то выберем любую из них. Минимальное расстояние от выбранной точки до прямой l₁ и есть наш способ выбор «крайнего» варианта, а выбранная точка – «крайний» вариант.
Выбранную точку обозначим буквой А₁.
Представим, что в выбранной точке пересекаются три прямые (см. условие задачи):

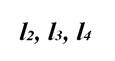
Эти три прямые, как нам известно, должны пересекать прямую l₁.
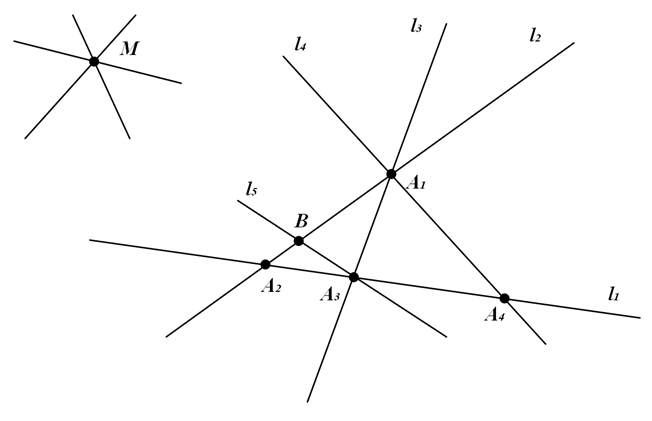
Точки пересечения обозначим, соответственно (см. рис.1):

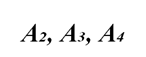
Через каждую из этих точек проходит по три прямые (см. условие задачи). Выберем, для примера, точку А₃, через которую проходит прямая l₅. Эта прямая пересекает прямую l₂ или l₄ (в зависимости от того, как мы её проведем) в некой точке В, которая ближе к l₁, чем А₁.
Мы получили противоречие, которое доказывает, что точка М – единственная точка пересечения прямых.

Решите другую задачу (задача №243):
Семь белок собрали вместе 100 орехов. При этом никакие две белки не собрали по одинаковому количеству орехов.

Необходимо доказать, что есть три белки, собравшие вместе не менее 50 орехов.

Решение задачи №243 можно посмотреть здесь: Правило расположения