Задачи №247, 248, 250

Первоначально решим задачу №248: У вас есть кран с водой и раковина для слива. Составьте схему получения одного литра воды с помощью 7-ми и 12-ти литрового сосуда.
Выполним операции НМ, ПМБ, ОБ (см. Переливания. Алгоритм решения. «Умный шарик» Я.И. Перельмана):

7:0 – 0:7 – 7:7 – 2:12 – 2:0 – 0:2 – 7:2 – 0:9 – 7:9 – 4:12 – 4:0 – 0:4 – 7:4 – 1:12

В меньшем сосуде (7-ми литровом) получаем требуемый литр воды.

Решим задачу №247: Можно ли решить задачу №245 (см. здесь: Переливания. Алгоритм решения. «Умный шарик» Я.И. Перельмана), если из крана разрешается наполнять только большой сосуд, а в раковину сливать воду только из малого сосуда. Составьте схему решения.
Если посмотреть наши обозначения в «Переливания. Алгоритм решения. «Умный шарик» Я.И. Перельмана», то можно заметить, что были введены сокращения (условные обозначения):

НБ – наполняем большой сосуд водой из-под крана;
ОМ – опорожняем малый сосуд, выливая воду в раковину (не в большой сосуд);
ПБМ – переливаем из большого сосуда в малый до наполнения последнего или до опорожнения первого.
Обозначения были введены, но небыли использованы.
Введем дополнительное условие:
БО? – проверить, опорожнен ли большой сосуд.

Составим схему исходя из указанных в задаче требований (рис. 1). Напомню, что мы используем обозначение количество воды в малом сосуде через М, а в большом – через Б. То есть количество воды в сосудах в ходе решения задачи можно записать как Б:М. У нас (см. задачу №245 и № 244) сосуды 5 и 3 литров.

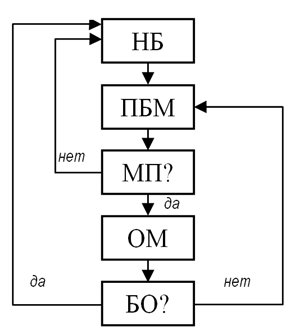
Составим цепочку, принимая первоначальное количество воды в сосудах равным нулю (сосуды пустые):
0:0 – 5:0 – 2:3 Мы получили 5, 2 и 3 литра
0:0 – 5:0 – 2:3 – 2:0 – 0:2 – 5:2 Мы получили 7 литров
0:0 – 5:0 – 2:3 – 2:0 – 0:2 – 5:2 – 4:3 Мы получили 4 литра
0:0 – 5:0 – 2:3 – 2:0 – 0:2 – 5:2 – 4:3 – 4:0 – 1:3 – 1:0 – 0:1 Мы получили 1 литр
0:0 – 5:0 – 2:3 – 2:0 – 0:2 – 5:2 – 4:3 – 4:0 – 1:3 – 1:0 – 0:1 – 5:1 – 3:3 Мы получили 6 литров
0:0 – 5:0 – 2:3 – 2:0 – 0:2 – 5:2 – 4:3 – 4:0 – 1:3 – 1:0 – 0:1 – 5:1 – 3:3 – 3:0 – 0:3 Мы получили 3 литра
0:0 – 5:0 – 2:3 – 2:0 – 0:2 – 5:2 – 4:3 – 4:0 – 1:3 – 1:0 – 0:1 – 5:1 – 3:3 – 3:0 – 0:3 – 5:3 Мы получили 8 литров
0:0 – 5:0 – 2:3 – 2:0 – 0:2 – 5:2 – 4:3 – 4:0 – 1:3 – 1:0 – 0:1 – 5:1 – 3:3 – 3:0 – 0:3 – 5:3 – 5:0 – 2:3
Обратите внимание, что в ходе переливаний мы не приходим обратно к позиции 0:0, как то было при первоначальном наполнении малого сосуда.

 Решим, используя «умный шарик» задачу №250: разделите пополам воду из 12-литровой емкости, используя емкости в 9-ть и 7-ть литров.
Ниже приведена схема движения шарика по нашему «бильярдному столу», сконструированному исходя из параметров задачи (рис. 2).

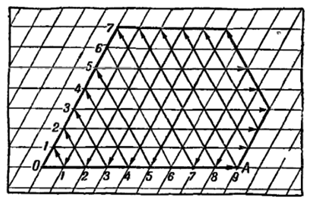
 Проследив за всеми передвижениями шарика, составим таблицу (рис. 3) ударов об борта (переливаний):

Шарик вернулся в точку O, так и не получив разделение 12-ти литров воды на две равные части в любой из комбинаций имеющихся сосудов. Это означает, что нельзя разделить пополам воду из 12-ти литровой емкости при помощи пустых сосудов в 9-ть и 7-мь литров.