Задачи №244, 245, 246, 247, 248, 249, 250

Бытует история, что известный французский математик Симон Пуассон^[1] в юности настолько заинтересовался предложенной ему задачей, что, увлекшись, посвятил свою дальнейшую жизнь математике.
Некто имеет двенадцать пинт^[2] вина и хочет подарить половину, но у него нет сосуда в шесть пинт. У него есть два пустых сосуда: один в 8 пинт, а другой в 5 пинт.
Спрашивается: каким образом налить шесть пинт вина в сосуд на восемь пинт?
Решение этой задачи (задача №56) вы можете найти здесь.

Можно попытаться решить задачу №17:
Имеются три сосуда вместимостью 8, 5 и 3 литра.
Первый заполнен водой, а два остальные – пустые.
Вопрос:
Как разлить воду в два из этих сосудов так, чтобы в каждом было по 4 литра?
Решение этой задачи вы можете найти здесь.

Или, например, задача №111:
У вас есть две емкости: 9 литров и 4 литра.
Необходимо используя эти емкости из бака набрать ровно шесть литров воды.
Примечание: в процессе воду можно сливать обратно в бак.
Решение этой задачи вы можете найти здесь.

Разберем, к примеру, решение постой задачи на переливание (задача №244):
Имеется два сосуда – трехлитровый и пятилитровый. Необходимо получить один литр воды, пользуясь указанными сосудами.
Воду мы наливаем из крана, а в раковину можно сливать излишки.

Решение, как уже указано, найти довольно просто. Мы наполняем трехлитровый сосуд и переливаем из него воду в пятилитровый. Вновь наполняем трехлитровый сосуд и переливаем из него воду в пятилитровый, пока не наполним последний до краев. В итоге у нас останется один литр воды в трехлитровом сосуде.

А что если нам необходимо получить не один, а два литра воды, три литра, четыре литра, пять, шесть, семь или восемь литров (задача №245).
Получить три, пять, восемь литров очень просто. Для этого необходимо наполнить один из сосудов (3 или 5 литров) или оба (8 литров).
Два литра мы получим отлив из полного пятилитрового сосуда в трехлитровый.
Если после этого вылить из трехлитрового сосуда воду, влить из него остатки (два литра) из пятилитрового сосуда, после чего наполнить пятилитровый сосуд, мы получим семь литров.
В трехлитровом сосуде остается место под еще один литр. Доливаем этот литр из пятилитрового сосуда, в котором останутся искомые четыре литра.
Выливаем воду из пятилитрового сосуда в раковину. Наполняем его тремя литрами из трехлитрового сосуда и вновь наполняем трехлитровый сосуд. Получаем шесть литров.

Задачи №244 и №245 можно решить устно, не особо при этом утруждаясь. Но при решении этих задач мы совершаем определенные шаги (операции), которые можно описать и даже изобразить в виде схемы. Для удобства описания введем сокращения (условные обозначения):

НБ – наполняем большой сосуд водой из-под крана;
НМ – наполняем малый сосуд водой из-под крана;
ОБ – опорожняем большой сосуд, выливая воду в раковину (не в малый сосуд);
ОМ – опорожняем малый сосуд, выливая воду в раковину (не в большой сосуд);
ПБМ – переливаем из большого сосуда в малый до наполнения последнего или до опорожнения первого;
ПМБ – переливаем из малого сосуда в большой.

Вопрос: какое количество воды нам удастся отмерить, если мы будем выполнять только операции (команды) НМ, ОБ, ПМБ? Дополнительным условием будет после ПМБ выполнять ОБ каждый раз, когда большой сосуд наполнится, и НМ, когда малый сосуд опорожнится. Если необходимо выполнить ОБ и НМ, то первоначально мы выполняем операцию ОБ.

Введенное дополнительное условие – это вспомогательные команды, которые мы обозначим следующим образом:
БП? – проверить, полон ли большой сосуд;
МО? – проверить, опорожнен ли малый сосуд.

Наглядно выполняемые нами операции удобнее изобразить в виде блок-схемы (рис.1).

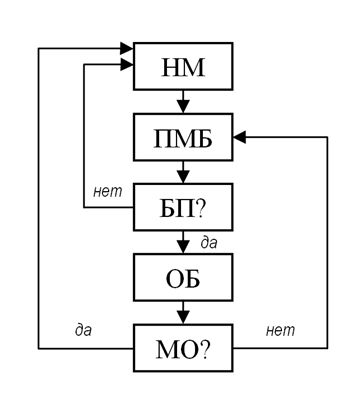
Мы получили определенный алгоритм[3] решения задачи.
Действуя по описанной схеме, мы переходим от одной операции к другой. Что касается вспомогательных команд, то условие для нашего перехода к другой операции (блоку) – полученный при выполнении вспомогательной команды результат. То есть мы выполняем условный переход[4].

 Если обозначить количество воды в малом сосуде через М, а в большом – через Б, то количество воды в сосудах в ходе решения задачи можно записать как М:Б.
Применительно к задачам №244 и №245 мы, действуя по указанной выше схеме, можем отмерить любое количество воды от одного до семи литров.
Например, принимая первоначальное количество воды в сосудах равным нулю (сосуды пустые), мы выстраиваем следующую цепочку:

0:0 – 3:0 Т.е. мы получили 3 литра.
0:0 – 3:0 – 0:3 – 3:3 Мы получили 6 литров.
0:0 – 3:0 – 0:3 – 3:3 – 1:5 – 1:0 Можно отмерить 1 литр.
0:0 – 3:0 – 0:3 – 3:3 – 1:5 – 1:0 – 0:1 – 3:1 Отмеряно 4 литра.
0:0 – 3:0 – 0:3 – 3:3 – 1:5 – 1:0 – 0:1 – 3:1 – 0:4 – 3:4 Получаем 7 литров.
0:0 – 3:0 – 0:3 – 3:3 – 1:5 – 1:0 – 0:1 – 3:1 – 0:4 – 3:4 – 2:0 Два литра.
0:0 – 3:0 – 0:3 – 3:3 – 1:5 – 1:0 – 0:1 – 3:1 – 0:4 – 3:4 – 2:0 – 3:2 Пять литров

Для завершения цепочки и перехода на новый цикл необходимо выполнить еще два действия:

0:0 – 3:0 – 0:3 – 3:3 – 1:5 – 1:0 – 0:1 – 3:1 – 0:4 – 3:4 – 2:0 – 3:2 – 0:5 – 0:0

Может показаться, что эти два действия лишние, так как у нас уже есть пять литров воды, а вылить воду в раковину можно первоначально из малого сосуда, а потом и из большого сосуда, не прибегая к переливанию из малого сосуда в большой. В действительности так бы и произошло, но мы пытаемся выстроить простую и удобную схему (алгоритм), которая позволит решать однотипные задачи. Построенная схема позволяет циклично получать результаты, отраженные в цепочке:

0, 3, 6, 1, 4, 7, 2, 5, 0

Если не требуется получать все результаты цепочки, что составленная нами схема потребует введения дополнительных условных переходов, связанных с необходимостью проверки выполнения требуемого нам условия.

 Решим, используя схему, следующую задачу (задача №246):
Можно ли отмерить 4 литра воды, используя сосуды емкостью девять и двенадцать литров? У нас есть кран с водой и раковина для слива воды.

Вполне очевидно, что общий делитель емкостей сосудов – 3. Как бы мы не переливали воду в емкостях, мы будем получать остаток в литрах, делимый на три.
Проверим на схеме:

0:0 – 9:0 – 0:9 – 9:9 – 6:12 – 6:0 – 0:6 – 9:6 – 3:12 – 3:0 – 0:3 – 9:3 – 0:12 – 0:0

Решите задачу №247: Можно ли решить задачу №245, если из крана разрешается наполнять только большой сосуд, а в раковину сливать воду только из малого сосуда. Составьте схему решения.
Решение задачи здесь: Переливания.

Решите задачу №248: У вас есть кран с водой и раковина для слива. Составьте схему получения одного литра воды с помощью 7-ми и 12-ти литрового сосуда.
Решение задачи здесь: Переливания.

Описанная выше схема позволяет решать задачи, в которых для измерения имеется два сосуда и емкость с водой (жидкостью), неограниченная по объему. Тем не менее, это достаточно простой и эффективный способ решения такого рода задач. Более того, это наглядное отражение возможности решения задач с помощью построения определенного алгоритма.
Для решения задач по переливанию с иными условиями (например, более двух емкостей), необходимо изменить (усложнить) схему, добавив дополнительные блоки (операции) и прописав условные переходы между ними.

Яков Исидорович Перельман[5] в свое время предложил в своей книге «Занимательная геометрия» весьма оригинальный и довольно простой способ решения задач на переливание для трех сосудов, больший из которых наполнен водой, с помощью воображаемого «умного» шарика и воображаемого «бильярдного» стола.
Представьте, что вам необходимо отделить некое количество воды из большего по объему сосуда, имея под рукой еще два сосуда меньшей емкости, неодинаковых по объему. Строим «бильярдный стол». Для этого берем молоток, гвозди, … Нет, конечно же. Наш инструмент – бумага и карандаш. С помощью этих инструментов рисуем на бумаге «бильярдный стол», по которому мы будем катить наш «умный шарик».
«Стол» будет представлять из себя многоугольник OADCB, состоящий из множества равных ромбов с острым углом в 60 градусов.
В качестве примера возьмем такие же емкости, которые были предложены Я.И. Перельманом в его книге «Занимательная геометрия», но обозначения «ведра» заменим на более привычные нам литры: 12 литров, 9 литров, 5 литров. Перед нами стоит вопрос (задача №249): разделить пополам воду из 12-литровой емкости, используя емкости в 9-ть и 5-ть литров.

Сторона OA будет численно равна сосуду в 9 литров – 9 единиц.
Сторона OB будет численно равна сосуду в 5 литров – 5 единиц.

Но нам необходимо определить размеры сторон AD, DC, CB. Сумма длин этих сторон будет численно равна, как можно догадаться, объему третьей емкости, то есть составит 12 единиц.

Сторона AD будет численно равна разности между объемами емкостей в 12 литров и в 9 литров:
12 – 9 = 3

Сторона CB будет численно равна разности между объемами емкостей в 12 литров и в 5 литров:
12 – 5 = 7

Сторона DC, соответственно, будет равна:
12 – 3 – 7 = 2

Важное примечание: Наполненная бочка всегда большая из трех. Если обозначить емкости пустых бочек через a и b, а наполненной через c, то при

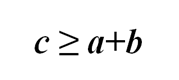
«биллиардный стол» следует строить в форме параллелограмма со сторонами a и b клеток.

Ниже приведена картинка из книги «Занимательная геометрия» (рис.2), на которой изображен полученный нами «бильярдный стол».

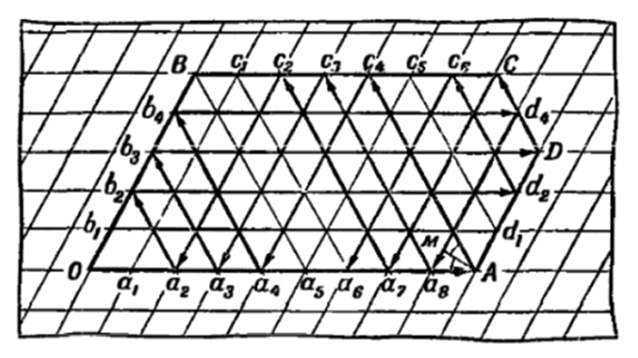
Если мы толкнем наш шарик вдоль длинной стороны OA, то он будет двигаться по столу, отскакивая от бортов.
В правом нижнем углу «стола» (рис. 2) вы можете увидеть разделение одного из «треугольников» на равные части, поясняющее прорисовку (закономерность) схемы движения шарика (указана стрелочками): «угол падения равен углу отражения».
Предлагаю «проследить» за движением шарика.
Каждая сторона разделена на соответствующее её длине количество единиц. Каждая точка пересечения линий внутри нашего стола отделена на определенное количество единиц от линий OA и OB.
Как только мы толкнули шарик от O вдоль стороны OA (начали наполнять 9-ти литровую емкость), он начнет проходить точки a₁, a₂, … то есть, каждая точка – это дополнительный литр в 9-ти литровой емкости. Деление есть на столе, но его нет на емкости, а потому шарик не останавливается на этих делениях, продолжая движение.
Оттолкнувшись от точки A (мы получили первые 9-ть литров), шарик начнет двигаться к стороне C. Напомню, что он движется по закону «угол падения равен углу отражения». Иначе говоря, из 9-ти литровой емкости мы переливаем воду в 5-ти литровую. Проход каждой точки от A к C обозначает, что в 9-ти литровой емкости количество жидкости уменьшилось на 1 литр, а в 5-ти литровой прибавилось на 1 литр. То есть, число единиц (клеток), на которые точка удалена от стороны OB, обозначает количество воды в 9-ти литровой бочке, а число единиц (клеток), на которые точка удалена от стороны OA, обозначает количество воды в 5-ти литровой бочке. Остальная вода, как вы понимаете, находится в 12-ти литровой бочке.

Проследив за всеми передвижениями шарика, мы можем составить таблицу:

Наша цель достигнута! Мы разделили воду из 12-ти литровой емкости пополам. Теперь в 9-ти литровой и 12-ти литровой емкости по 6 литров.

Примечательно, что если вы толкнете шарик от точки O вдоль стороны OB (сначала наберете 5 литров), остановите (!) в точке B, а затем толкнете по BC, предоставив ему возможность далее двигаться самостоятельно, отталкиваясь от бортов, то решить задачу можно гораздо более коротким путем. Можете прорисовать схему и посчитать количество ходов от точки O (количество переливаний), необходимых для достижения цели – разделения 12-ти литров пополам.
В случае, если шарик продолжит свой путь, то он пройдет все вершины ромбов, что означает, что из 12-литровой емкости можно отлить в 9-ти литровую емкость любое количество воды от одного до 9-ти, а в пятилитровую – от одного до пяти.

Возможны варианты, когда задача не имеет решения (по аналогии с задачей №246). Попробуйте решить, например, составив схему движения шарика и соответствующую таблицу, такую задачу (задача №250): разделите пополам воду из 12-литровой емкости, используя емкости в 9-ть и 7-ть литров.
Решение задачи здесь: Переливания.

Предложенный Я.И. Перельманом способ позволяет ответить на два важных вопроса:

1. Можно ли установить определенный порядок переливаний, которого можно придерживаться во всех случаях, независимо от емкости сосудов.
2. Можно ли при помощи двух пустых сосудов отлить из третьего любое возможное количество воды.

При решении задач на переливание с помощью описанных выше способов можно столкнуться с тем, что применение указанных способов ведет к ответу более длинным путем, чем мы смогли бы найти, действуя интуитивно. Но важность построения различных схем и алгоритмов решения задач состоит не в первоначально достигаемой скорости, с которой мы приходим к решению, а в самой возможности построения безошибочного алгоритма (схемы), применяемой при решении и, следовательно, к дальнейшей возможности машинной обработки тех или иных однотипных задач.

[1]    Симон Дени́ Пуассо́н (21 июня 1781 – 25 апреля 1840) – французский математик, механик, физик.

[2]    Пи́нта – единица объема в английской системе мер. Британская пинта равна 34,677 кубических дюйма или 568,261 миллилитра.

[3] Алгори́тм (латинское  algorithmi — от имени среднеазиатского математика Аль-Хорезми) – совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения определённой задачи. См. также Немного об алгебре.

[4] Условный переход – команда на изменение порядка выполнения программы в соответствии с результатом проверки некоторого условия.

[5] Яков Иси́дорович Перельма́н (4 декабря 1882 – 16 марта 1942) – русский и советский математик, физик, журналист, педагог, популяризатор точных наук.