История развития способа записи цифр и чисел

Проблема записи цифр и чисел с помощью знаков стояла перед человеком с самых древних времен. По мере роста практической потребности и эволюции математической мысли всё более актуальной становилась задача изобразить употребляемые числа при помощи наименьшего количества знаков (цифр).

У разных народов были различные пути решения этой задачи.

На рисунке 1 представлено два варианта написания цифр в древнем Египте. Верхние две строчки написаны иероглифами. Нижняя строка – иератическими знаками[1].

Рисунок 1

На рисунке 2 уравнение, записанное иероглифическим письмом.

_{Рисунок 2 Обратите внимание на первый и третий символ справа. Первый справа символ очень похож на R2-D2 (Звездные войны), а третий справа вообще НЛО с гуманоидом, взлетающая вверх!!! Пояснение смотри в «Цифры и конспирология«}

Читается уравнение справа налево: «Куча (неизвестное), ⅔, ½, ⅐, целое (кучи) составляет 33». В переложении на современный способ записи: х+⅔х+½х+⅐х=33.

На рисунке 3 представлены китайские цифры, использовавшиеся в ученых трактатах, а на рисунке 4 – китайские коммерческие цифры и примеры написания чисел.

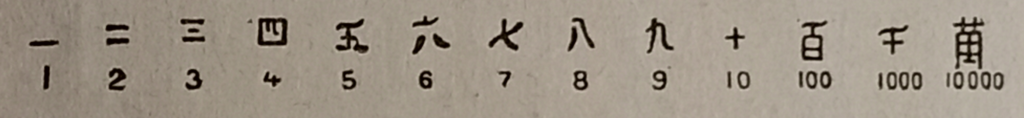
Рисунок 3

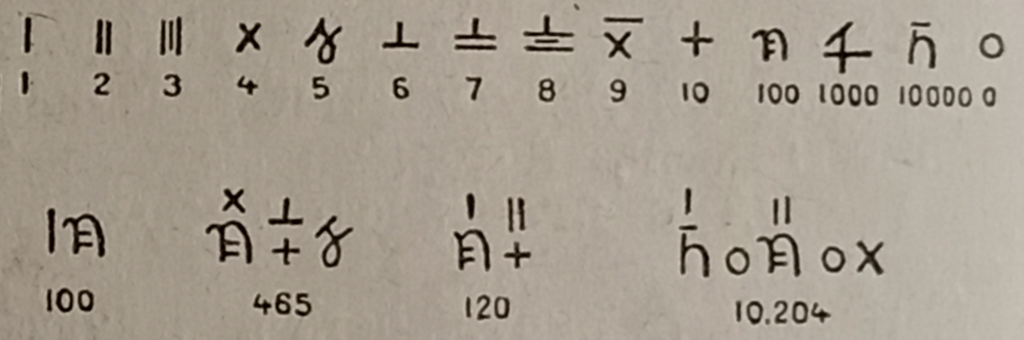
Рисунок 4

На рисунке 5 представлена славянская нумерация[2].

Рисунок 5

В обычной жизни люди обходились так называемым «малым счетом» (см. рис.5 и рис.6 («Тысяща»)). «Малый счет» доходил до числа 10 000, которое в самых ранних памятниках называется «тьма», то есть темное число, которое нельзя ясно представить. В дальнейшем была принята к употреблению дополнительная система, называемая «числом великим словенским» (рисунок 6).
В нем употреблялись такие разряды:

• Тьма — 10⁶;
• Легеон — 10¹²;
• Леодр — 10²⁴;
• Ворон — 10⁴⁸;
• Колода (десять воронов) — 10⁴⁹

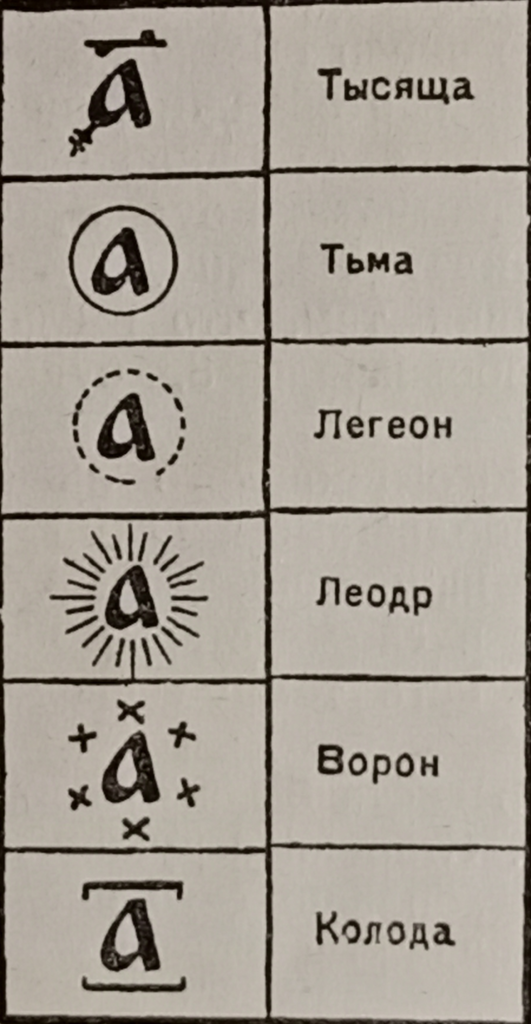
Рисунок 6

Об эволюции понятия числа можно прочитать здесь.

Широко известны и до настоящего времени применяются римские обозначения цифр: I, II, III, IV, V и т.д. Мы широко пользуемся числами на основе римской нумерации при обозначении размеров одежды или веков: XL, XV и т.д.

Идеальным решением вопроса явилось изобретение поместной (позиционной) нумерации, то есть такого способа изображения чисел, в котором одна и та же цифра означает различные разряды, в зависимости от занимаемого места (позиции). Сейчас, используя поместную систему нумерации мы, благодаря существованию нуля, можем записать любое число при помощи десяти цифр.

Стоит отметить, что поместная (позиционная) нумерация начала формироваться очень давно. Зародившаяся в древнем Шумере[3] в III тысячелетии до н.э. и унаследованная Вавилонским царством[4] шестидесятеричная система счисления[5] уже имела позиционную нумерацию. На рисунке 4 представлен пример шумерских цифр (верхняя строка) и вавилонских цифр (нижняя строка). Вавилоняне создали совершенное для своего времени счисление, в основе которого лежало не число 10, а число 60, что во многом облегчало труднейшее арифметическое действие – деление. Нынешнее деление круга на 360 градусов, деление часа на 60 минут, минут на 60 секунд – наследие древнего Вавилона.

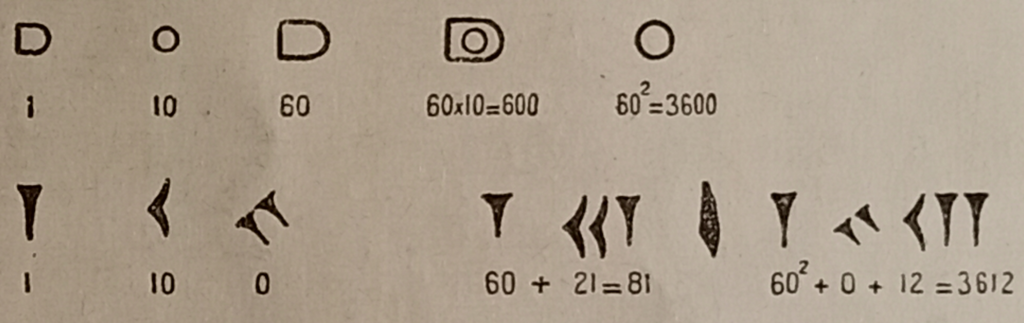
Рисунок 7

Народы Урарту (Ванского царства)[6], усвоив математику захваченного ими Вавилона, переработали её, перейдя к десятичной нумерации, близкой к нынешней позиционной десятичной. Используемая ими система нумерации резко отличалась от египетской десятичной нумерации, не имевшей позиционного принципа.

Установлению современной системы цифр способствовало открытие книгопечатания[7] в середине XV столетия. До этого цифры не имели стандартной формы.

Существует множество теорий, объясняющих нынешнюю форму цифр. Изучению данного вопроса посвящали время не только ученые-математики, но и ученые-историки, а так же те, чья деятельность отнюдь не была связана с математикой. Например, у А.С. Пушкина можно найти такую заметку, сопровождаемую чертежом (рисунок 8).

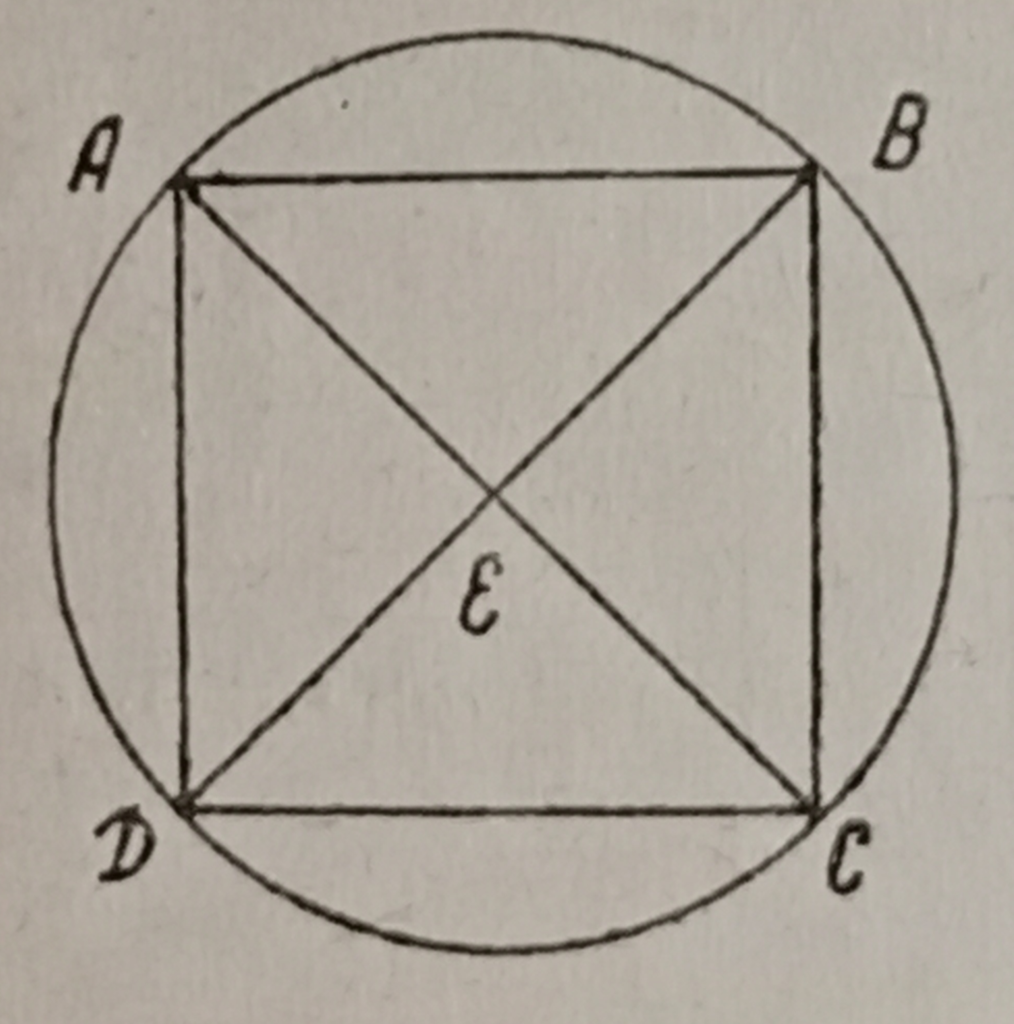
Рисунок 8

«Форма цыфров арабских составлена из следующей фигуры
AD (1), ABDC (2), ABECD (3), ABD+AE (4)».

Догадка А.С. Пушкина отражена среди прочих попыток пояснить происхождение формы цифр на рисунке 9 под номером VII.

Рисунок 9

Распространенное наименование используемых в настоящее время цифр – арабские. Это не совсем верно. Правильнее называть их индусскими (индийскими), так как именно используемые индусами начертания цифр легли в основу привычного нам написания, сильно при этом эволюционировав (рисунок 10). На это обстоятельство в середине XVIII века указывал в своих работах востоковед Георгий Яковлевич Кер[8].

Рисунок 10

В России индусские цифры появляются в конце XVII века. Они применяются параллельно со славянскими цифрами, что и находит отражение на гравюрах и рукописях. Начиная с «Арифметики»[9] Леонтия Филипповича Магницкого[10], в математических книгах в России используются только индусские цифры.

Одну из задач, приведенных в «Арифметике» Л.Ф. Магницкого, вы можете посмотреть здесь и попытаться решить.

[1]    Иерати́ческое письмо – одна из форм египетского письма.

[2]    В качестве примера приведен способ записи кириллицей. Существовал и способ записи глаголицей.

[3]    Шуме́р – древняя область в Южной Месопотамии на территории современного Ирака.

[4]    Вавилонское царство (Вавило́ния) – древний регион и царство между Тигром и Ефратом на юге Месопотамии (территория современного Ирака), возникшее в начале II тысячелетия до н.э.

[5]    Шестидесятери́чная систе́ма счисле́ния – позиционная система счисления по целочисленному основанию 60.

[6]    Ура́рту (Ва́нское ца́рство) – древнее государство, располагавшееся на территории Армянского нагорья и занимавшее главенствующее положение среди государств Передней Азии в первой четверти I тысячелетия до н.э.

[7]    Годом изобретения книгопечатания считается 1445 год – начало использование литер при печати. Следует отметить, что первой печатной книгой считают текст, созданный с помощью ксилографии в Корее в период с 704 по 751 год.

[8]    Георг-Якоб (Георгий Яковлевич) Кер (27 июля 1692 – 5 мая 1740) – востоковед.

[9]    «Арифметика» (А҆рїѳме́тїка, си́рѣчь наꙋ́ка числи́телнаѧ. С̾ра́зныхъ дїале́ктѡвъ наславе́нскїй ꙗ҆зы́къ преведе́наѧ, и҆ во є҆ди́но собрана̀, и҆ на двѣ̀ кни́ги раздѣле́на) – первый печатный курс математики на книжно-славянском языке. Издана в 1703 году.

[10] Магни́цкий Лео́нтий Фили́ппович (19 июня 1669 – 30 октября 1739) – русский математик, педагог. Фамилия при рождении – Телятин или Теляшин.

Смотри статью «Цифры и конспирология».