Комната с коврами

Решите следующую задачу:
Пол помещения площадью 12 м² покрыт тремя коврами. Площадь первого ковра 5 м², второго – 4 м², третьего – 3 м². 
Каждые два ковра перекрываются на площади 1,5 м², причем 0,5 м² из этих полутора квадратных метров приходится на участок пола, где перекрываются сразу все три ковра.
Необходимо:

• найти площадь пола, не покрытую коврами;
• найти площадь участка, покрытого одним только первым ковром.

Использовать для решения этой задачи мы будем способ, предложенный в XVIII веке Леонардо Эйлером[1], а впоследствии доработанный Джоном Венном[2]. Более подробно мы останавливались на этом при рассмотрении решения к задаче №166.

Перейдем к решению нашей задачи.
Первоначально переведем условия задачи на язык математики. И помещение, и ковры, описанные в условиях задачи, измеряются в квадратных метрах. То есть, мы имеем дело с одинаковыми единицами измерения, что существенно облегчает для нас поиск ответа, так как отсутствует необходимость перевода в сравнимые единицы.
Наше помещение – это некое множество квадратных метров.
Каждый ковер – подмножество квадратных метров, которое располагается строго внутри нашего множества (см. условие задачи).
Из условий задачи следует, что имеются пересечения подмножеств внутри множества (ковры перекрывают друг друга).
Для нас не имеет никакого значения форма комнаты, а также форма ковров. Чтобы избежать путаницы, обозначим ковры буквами:
А – ковер площадью 5 м²;
Б – ковер площадью 4 м²;
С – ковер площадью 3 м². 
Комнату обозначим буквой К.
Пересечение подмножеств обозначим комбинацией соответствующих букв.
Рисуем нашу схему:

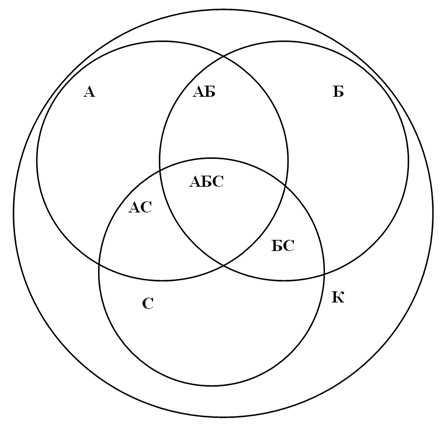
Впишем в каждую часть схемы то количество квадратных метров, которое занимает конкретный участок (сектор).
Из условий задачи следует, что каждые два ковра перекрываются на площади 1,5 м², причем 0,5 м² из этих полутора квадратных метров приходится на участок пола, где перекрываются сразу все три ковра.
Значит:

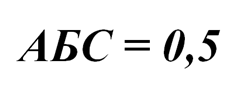
Площадь, на которой пересекаются ковры А и Б, но не пересекаются с ковром С, уменьшается на АБС. Аналогично и для пересечений А и С, а также Б и С.

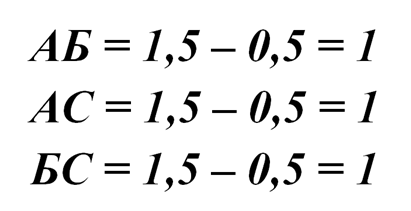
Найдем площадь ковра А, которая не пересекается с другими коврами. Она равна

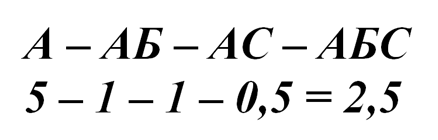
Аналогично для ковра Б:

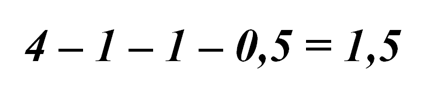
И для ковра С:

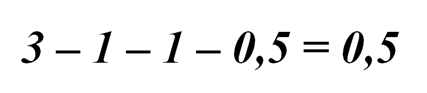
Нам необходимо найти площадь комнаты, которая осталась непокрыта коврами. Она равна

К – 2,5 – 1,5 – 0,5 – 1 – 1 – 1 – 0,5 = 4

Наша схема приобрела следующий вид

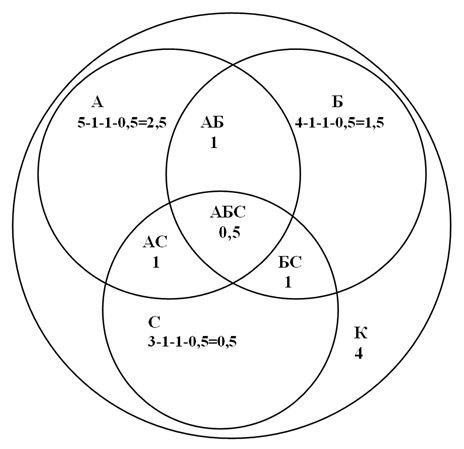
Мы получили ответы на поставленные в задаче вопросы:
Площадь пола, не покрытая коврами, составляет 4 м².
Площадь участка, покрытого одним только первым ковром, составляет 2,5 м².

Надоели «круги Эйлера»? Развлеките себя решением такой задачи (задача №171 «Недружелюбные соседи»):
Жители пяти домов поссорились друг с другом и, дабы не встречаться у колодцев, решили «поделить» колодцы между собой так, чтобы хозяин каждого дома ходил к «своему» колодцу по «своей» тропинке.
Как расположены дома, колодцы и тропинки, смотрите здесь:

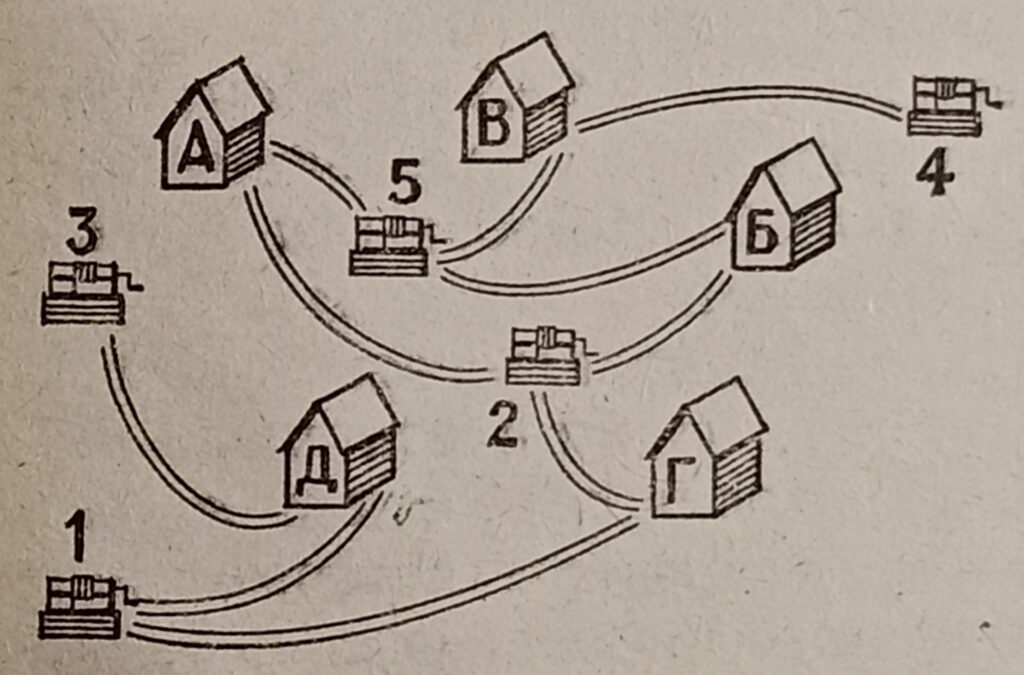
Условие: Новые тропинки не делаем!
Ответ смотрите здесь: «Графы«.

[1]     Леона́рд Э́йлер (15 апреля 1707 – 7 сентября 1783) – швейцарский, прусский и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук. Также внес значительный вклад в развитие физики, астрономии и других наук.

[2]    Джон Венн (4 августа 1834 – 4 апреля 1923) – английский логик и философ.