Задача №172. Любители шахмат

В качестве разминки после задачи №170 «Комната с коврами» была приведена задача №171 «Недружелюбные соседи». Задача очень простая. Ответом на неё может быть такой вариант: В4, А5, Б2, Г1, Д3. Может быть вариант с Б5 и А2.
Для нас имеет значение не сам ответ, а способ, с помощью которого он найден – соединение отрезками различных исходных точек и конечных объектов. В задаче №171 исходные точки – дома, конечные объекты – колодцы, а тропинки – отрезки, с помощью которых соединяются наши исходные точки.
Если перевести на язык математики, то мы имеем множество объектов, между которыми необходимо установить парную связь, например, «дом – колодец». Иными словами, мы имеем дело с графом – множеством точек (вершин графа), которые соединены между собой линиями (ребрами графа). Ребра графа – это не всегда прямолинейные отрезки. Довольно часто это дуги (см. задачу №171).
Теория графов имеет огромное научное и прикладное значение. Самые простые научные примеры – изображение многогранников или структурных формул химических соединений. В жизни мы встречаем графы в виде маршрутов движения воздушных судов или железнодорожных составов, где вершинами графа являются города, а рёбрами — рейсы, соединяющие пары городов.
Для понимания того, насколько просто разрешаются некоторые вопросы при использовании теории графов, предлагаю решить такую задачу (задача №172):
Шесть любителей шахмат собрались в парке, чтобы сыграть друг с другом по одному разу. Назовем их так: Алексей, Борис, Василий, Герман, Дмитрий, Егор. Имена специально подобраны в алфавитном порядке, для простоты дальнейшего обозначения.
Через некоторое время были проведены следующие игры:

• Алексей сыграл с Борисом, Германом и Егором;
• Борис, кроме того, что сыграл с Алексеем, сыграл еще и с Германом;
• Василий сыграл с Германом, Дмитрием и Егором;
• Герман сыграл с Алексеем и Борисом;
• Дмитрий сыграл с Василием;
• Егор сыграл с Алексеем и Василием.

Вопросы задачи звучат так:

1. Сколько игр уже проведено?
2. Сколько игр осталось провести?

Для начала изобразим уже сыгранные партии в виде схемы (рис. 1). При этом имена игроков будем обозначать только одной буквой – первой буквой имени возле точки, обозначающей игрока. Каждых двух сыгравших между собой игроков соединим отрезками.

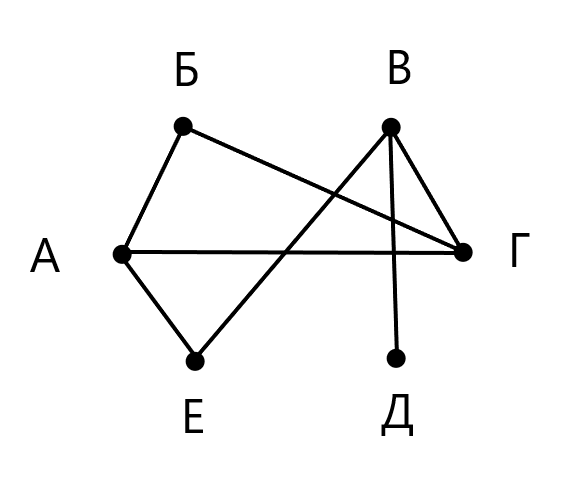
Мы получили схему, называемую граф. Наши игроки (точки) – вершины графа, а соединяющие их отрезки – ребра графа. Стоит отметить, что места пересечения ребер графа вершинами графа не являются. Чаще всего вершины графа изображают не точками, а небольшими кружками, которые визуально отличаются от точек. Это позволяет избежать путаницы между вершинами графа и местами пересечения ребер графа. Также в кружки могут вносить необходимые обозначения.

Полученная нами схема дает наглядное представление о том, какие игроки между собой уже сыграли и о количестве сыгранных партий. В нашем случае граф имеет семь ребер, то есть сыграно семь партий.

Теперь мы нарисуем схему, на которой пунктирными линиями соединим игроков, еще не сыгравших между собой (рис. 2):

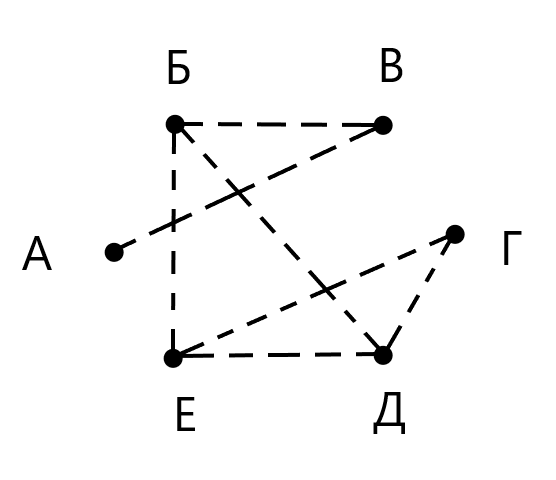
У этого графа восемь ребер. Значит, осталось провести еще восемь игр.

Широко известна «задача о Кёнигсбергских мостах». Статья Леонарда Эйлера (см. «Круги Эйлера») «Решение одной задачи, связанной с геометрией положения» о решении задачи о кёнигсбергских мостах опубликована в 1736 году, в связи с чем этот год считается годом рождения теории графов.
Эйлер в своей статье формулирует задачу так:
«В городе Кенигсберге, в Пруссии, есть остров, называемый Кнайпхоф; река, окружающая его, делится на два рукава, что можно увидеть на рисунке. Рукава этой реки пересекают семь мостов а, b, с, d, e, f и g. В связи с этими мостами был поставлен вопрос, можно ли совершить по ним прогулку так, чтобы пройти по каждому из этих мостов, причём ровно по одному разу».

Рисунок из статьи Леонарда Эйлера «Решение одной задачи, связанной с геометрией положения» (рис. 3):

В статье Эйлер формулирует метод решения: «Весь мой метод основан на надлежащих обозначениях для отдельных прохождений мостов. Я использую заглавные буквы А, В, С, D для обозначения отдельных областей, на которые река разделяет сушу. Таким образом, если некто движется из области А в область В через мост а или b, то я обозначаю прохождение моста символом АВ».
Способ решения подобных задач Эйлер описывает так:
«…в каждом возможном случае следующее правило позволяет непосредственно и без труда выяснить, можно ли осуществить прогулку по всем мостам без повторений:
Если имеется более двух областей, в которые ведёт нечётное число мостов, можно заявить с уверенностью, что такая прогулка невозможна.
Если, однако, имеются только две области, в которые ведёт нечётное число мостов, то прогулка осуществима при условии, что она начинается в одной из этих двух областей.
Если, наконец, нет ни одной области, в которую ведёт нечётное число мостов, прогулка с требуемыми условиями осуществима, причём начинаться она может в любой области.
Следовательно, с помощью этого правила поставленная задача может быть полностью решена».
То есть, задача о кёнигсбергских мостах не имеет решения, поскольку в графе этой задачи нечётную степень имеют четыре вершины. Сам Эйлер так формулирует ответ к задаче:
«Следовательно, в случае с кёнигсбергскими мостами, поскольку на остров А ведут пять мостов а, b, с, d, e, необходимо, чтобы буква А встретилась в описании движения по этим мостам трижды. Кроме того, дважды должна встретиться буква В, так как в область В ведут три моста, и буквы D, C должны встретиться по два раза каждая. Поэтому в последовательности из восьми букв, с помощью которой описывается рассматриваемый маршрут, проходящий через семь мостов, буква А должна встретиться три раза, а каждая из букв В, D, C — по два раза. Такого, однако, в последовательности из восьми букв быть не может. Таким образом, ясно, что подобная прогулка по семи мостам Кёнигсберга невозможна».
Собственно, сам граф выглядит следующим образом (рисунок 4):

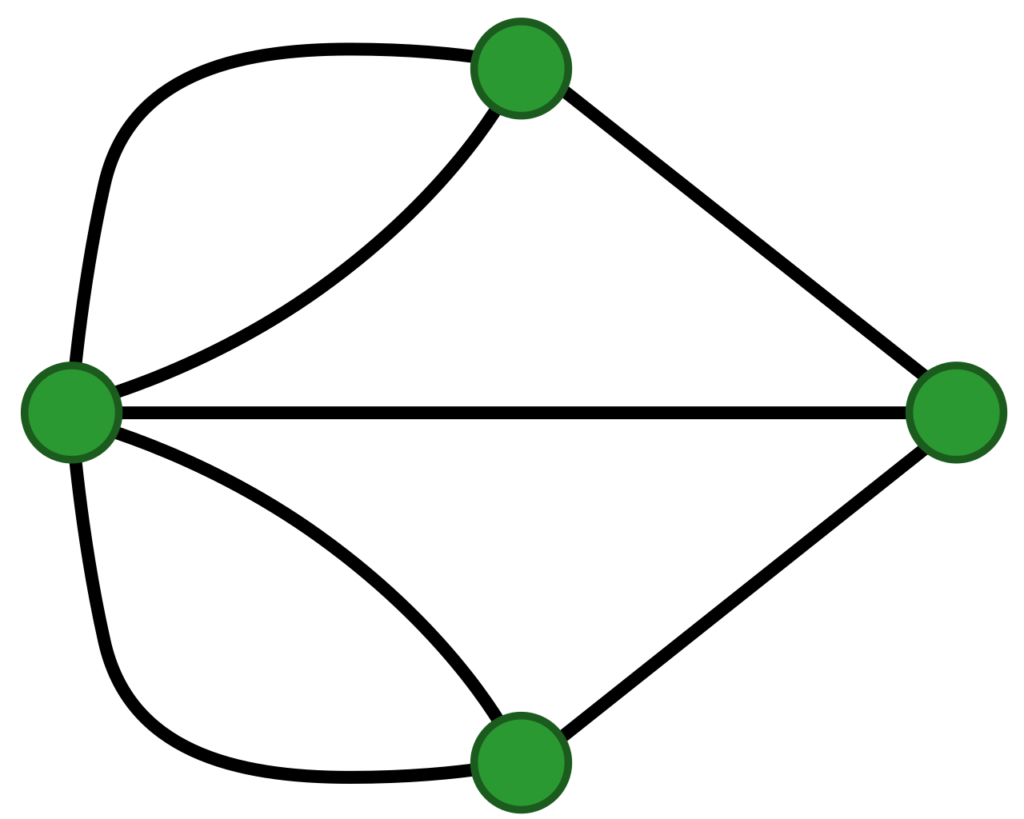
Если двигаясь вдоль ребер графа можно из любой его вершины попасть в любую другую, то такой граф называется связным. Если же в каждой вершине связного графа сходится четное количество ребер, то такой граф называется «эйлеров». Всякий эйлеров граф допускает непрерывный замкнутый обход (такой путь в теории графов имеет свое название – цикл), проходящий по каждому ребру ровно один раз.

Попытайтесь решить такую задачу (задача №173): не отрывая карандаша от бумаги и не проводя по какому-либо ребру дважды, нарисуйте граф, изображенный на рисунке 5. Пронумеруйте ребра в той последовательности, в которой вы их проходили.

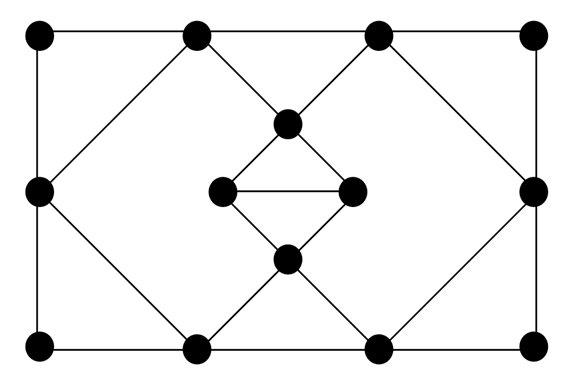
Ответ к задаче №173 здесь.