Задача №173

Нам необходимо решить такую задачу (задача №173): не отрывая карандаша от бумаги и не проводя по какому-либо ребру дважды, нарисуйте граф, изображенный на рисунке (рис.1). Пронумеруйте ребра в той последовательности, в которой вы их проходили.

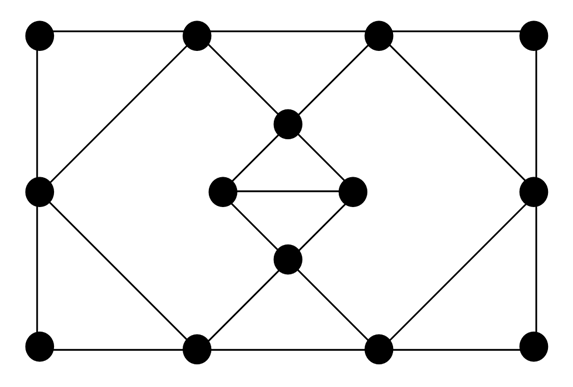
При разборе задачи «о Кёнигсбергских мостах» (см. «Графы») Леонард Эйлер сформулировал следующие правила решения задач с «обходом графов»:

1. Если имеется более двух областей, в которые ведёт нечётное число мостов, можно заявить с уверенностью, что такая прогулка невозможна.
2. Если, однако, имеются только две области, в которые ведёт нечётное число мостов, то прогулка осуществима при условии, что она начинается в одной из этих двух областей.
3. Если, наконец, нет ни одной области, в которую ведёт нечётное число мостов, прогулка с требуемыми условиями осуществима, причём начинаться она может в любой области.

В нашем графе есть вершины с четным количеством сходящихся «мостов» (ребер), а также есть вершины с нечетным количеством сходящихся «мостов» (ребер). Причем, у нас именно две вершины графа с нечетным количеством сходящихся ребер (см. центр графа). Иначе говоря, у нас всего две вершины с нечетной кратностью. Кратность вершины – это число ребер, сходящихся в этой вершине.
Если исходить из правила №2, сформулированного Эйлером, то обход графа (решение нашей задачи) возможен, причем мы должны начать обход графа именно от одной из двух вершин, имеющих нечетное количество сходящихся ребер.
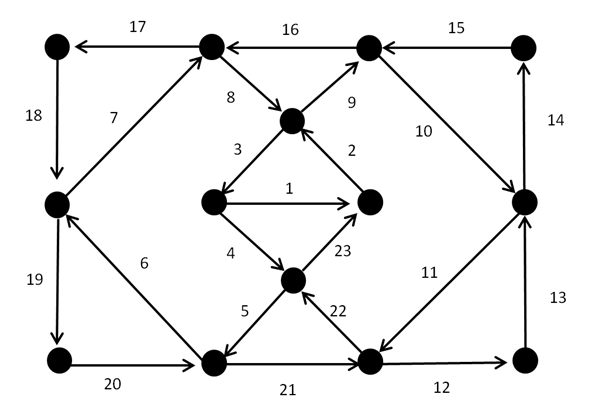
Исходя из сформулированного выше пояснения, вы можете проделать собственный путь по графу. Одно из возможных решений приведено на рисунке 2:

В качестве тренировки «обойдите» граф, изображенный на рисунке 3 (задача №174). Условия аналогичны условиям задачи №173: проходить граф необходимо не отрывая карандаша от бумаги и не проводя по какому-либо ребру дважды.

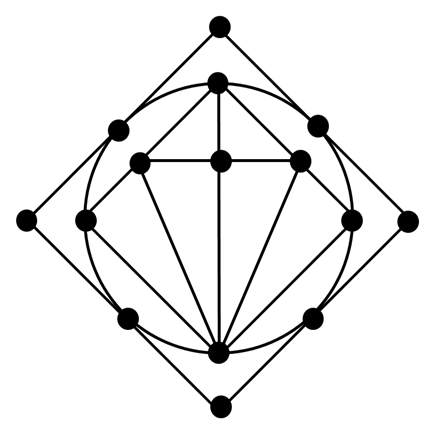
Решение к задаче №174 здесь: Арифметика остатков.