Задача №175

В задаче №174 (см. в тексте задачи №173) нам необходимо было «обойти» граф, изображенный на рисунке 1. Условия: проходить граф необходимо не отрывая карандаша от бумаги и не проводя по какому-либо ребру дважды.

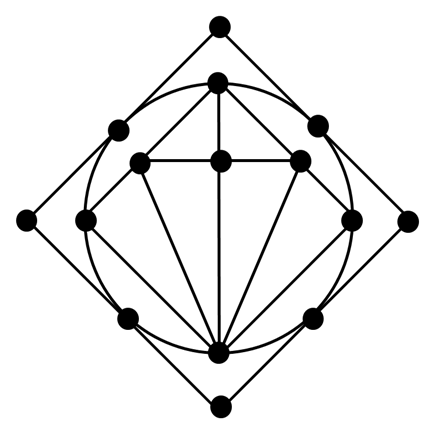
Один из возможных вариантов обхода изображен на рисунке 2:

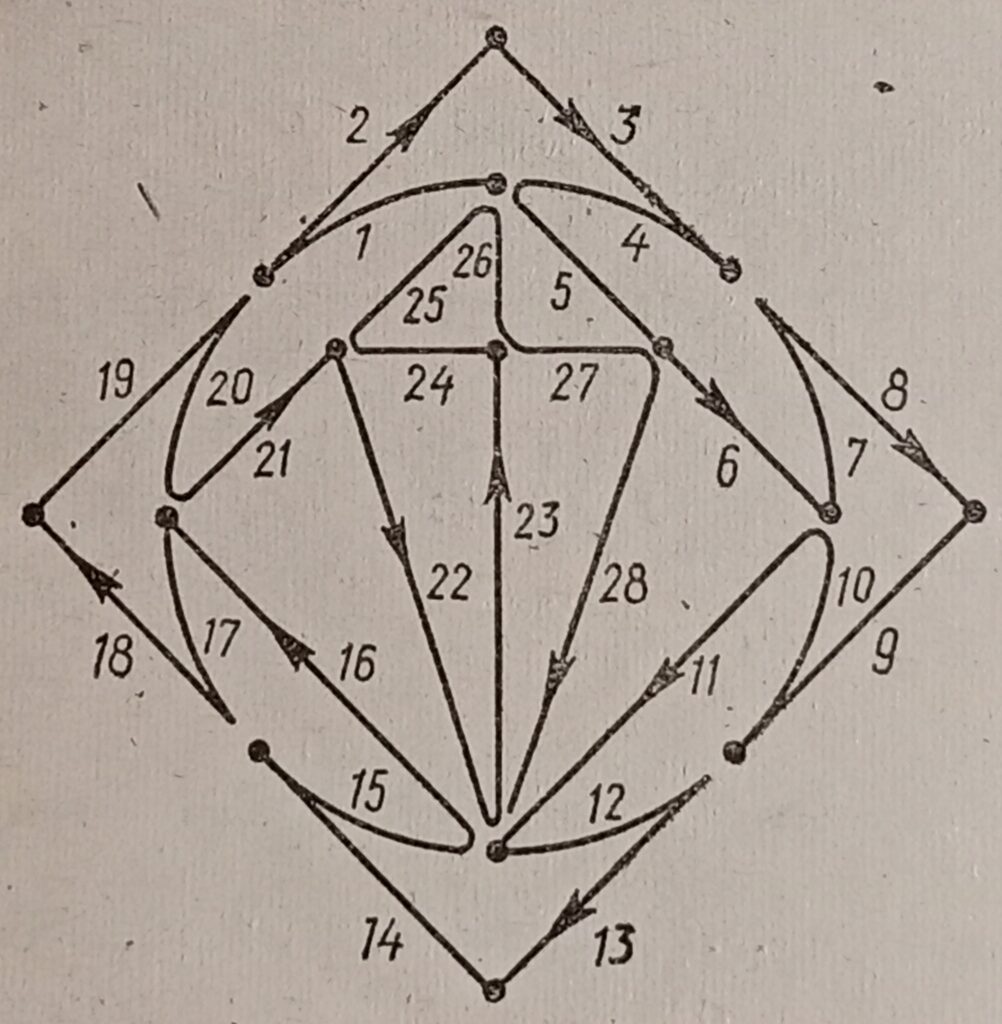
При, казалось бы, игровой направленности «обхода» графов, решение задач по «обходу» имеет и вполне прикладное значение.
Например, мы ставили перед собой задачу обхода каждого ребра графа, опираясь на то, что всякий эйлеров граф (см. «Графы») допускает непрерывный замкнутый обход (цикл), проходящий по каждому ребру ровно один раз. Но имеется еще и гамильтонов цикл, то есть такой цикл (замкнутый путь), который проходит через каждую вершину данного графа ровно по одному разу. Граф, содержащий гамильтонов цикл, носит название гамильтонов граф.
С гамильтоновым графом тесно связано понятие гамильтонова пути – простого пути (пути без петель), проходящим через каждую вершину графа ровно один раз. Отличия гамильтонова цикла от гамильтонова пути в том, что у пути начальные и конечные точки могут не совпадать, в отличие от цикла. Гамильтонов цикл, как вы понимаете, является гамильтоновым путём, а гамильтонов путь не всегда будет циклом.
Все эти названия (гамильтонов граф, гамильтонов путь, гамильтонов цикл)  даны в честь ирландского математика Уильяма Гамильтона[1], который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру. Путешествующий должен пройти «вокруг света», найдя путь, который проходит через все вершины ровно один раз.
Линия для додекаэдра, предложенная Гамильтоном для замены его игры «вокруг света» на додекаэдре на задачу для плоского графа изображена на рисунке 3:

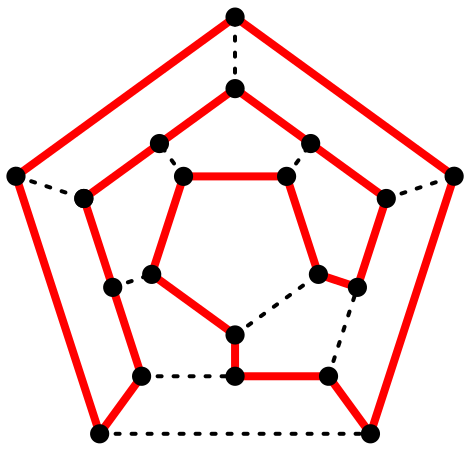
В данном случае мы имеем дело с примером решения задачи, связанной с логистикой – обеспечением организации движения материальных и иных ресурсов.

Прикладное значение отдельных математических тем не всегда очевидно, но уже само расширение кругозора, полученное при изучении новых тем, дает неоценимый вклад в собственное развитие.

Решите, например, в уме такую задачу (задача №175):
Найдите остаток от деления на 7 суммы чисел:

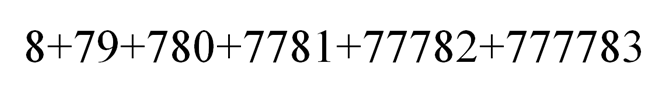
Для решения этой задачи рассмотрим таблицу на рисунке 4:

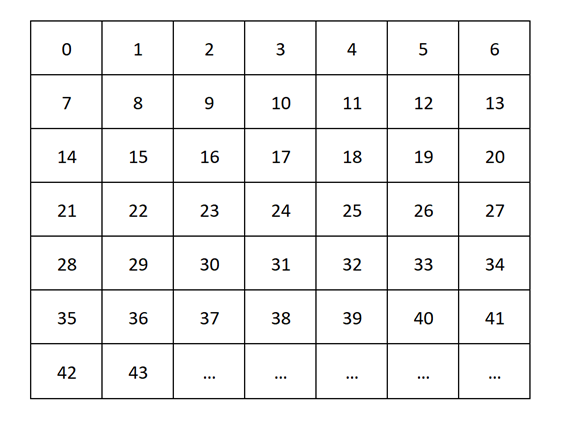
Многоточие в данном случае обозначает, что все последующие числа расположены по единому для всей таблицы принципу. Принцип этот весьма прост. Все целые неотрицательные числа выписаны подряд, при этом, за исключением первой строки таблицы, действуют правила:

• числа в первом столбце делятся на семь без остатка;
• числа второго столбца делятся на семь с остатком 1;
• числа третьего столбца делятся с остатком 2;

и так далее. Первая строка таблицы показывает нам тот остаток, который мы получаем при делении на семь.
В арифметике остаток — это целое число, «оставшееся» после деления одного целого числа на другое для получения целочисленного частного. То есть, последующее деление остатка на делитель приводит к получению дробной части.
Аналогичную таблицу можно нарисовать для двойки, тройки, пятерки и т.д.
В нашей таблице натуральное число 7 – делитель для всех чисел в таблице или модуль, по которому мы проводим сравнение целых чисел в таблице. Иными словами, мы проводим математическую операцию сравнения по модулю, позволяющую ответить на вопрос о том, дают ли два выбранных целых числа при делении на модуль один и тот же остаток.
Числа, дающие при делении на модуль (для нашей таблицы это 7) одинаковые остатки, называются «сравнимыми по модулю» или «равноостаточными». То, что некие числа А и В при делении на модуль М дают одинаковые остатки, то есть являются сравнимыми по модулю М, можно записать следующим образом:

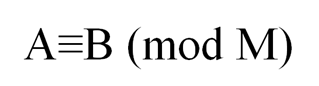
Знак «≡» обозначает сравнение по модулю в теории чисел, а также используется как знак тождественного равенства в математике, как знак операции эквивалентности в логике (о других знаках математики см. также Знаки равенства и неравенства, Строгие и нестрогие неравенства).

Отношение сравнимости (по данному модулю) является отношением эквивалентности. Это означает выполнение трёх свойств:
рефлексивность: каждое число эквивалентно самому себе;
симметричность: если А эквивалентно В, то В эквивалентно А;
транзитивность: если А и В эквивалентны С, то А эквивалентно В.
Эти три свойства гарантируют возможность разбиения всех объектов на непересекающиеся классы эквивалентности, при этом элементы одного класса будут эквивалентны друг другу, а разных — нет.

Как уже было указано выше, мы можем выбрать в качестве модуля любое натуральное число, но модуль для решения нашей задачи — число 7.

В нашей таблице числа разбились на семь групп (столбцов), каждая из которых отвечает определённому остатку от деления на наш модуль. Такие группы носят название классов или классов вычета по модулю.
Чтобы узнать, к какому классу относится число, надо найти остаток от деления этого числа на модуль (в нашем случае – на семь). Остаток будет равен индексу класса. Первая строка нашей таблицы отражает индексы классов, на которые и идет разделение классов: 0, 1, 2, 3, 4, 5, 6.
Вывод первый: В один и тот же класс попадают все числа, дающие при делении на модуль один и тот же остаток.
Вывод второй: Два числа принадлежат к одному классу тогда и только тогда, когда их разность делится без остатка на модуль (можете проверить это по столбцам таблицы). Например, рассмотрим числа одного класса:
20 – 13 = 7
Семь делится на семь без остатка, а поэтому оба наши числа принадлежат к одному классу.
Возьмем другие два числа:
41 – 13 = 28
28 делится на семь без остатка.
Если мы суммируем выбранные числа, то получим:
20+13=33. Остаток при делении на 7 равен 5.
41+13=54. Остаток при делении на 7 равен 5.
Это означает (вывод третий), что остаток от деления на модуль не измениться при замене одного или каждого слагаемого другим числом того же класса, в частности, индексом этого класса:
6+41=47. Остаток при делении на 7 равен 5.

Но мы еще не решили нашу задачу. Чему же будет равен остаток от деления на 7 суммы чисел: 8+79+780+7781+77782+777783 ?

Используя таблицу для модуля 7, проанализируем числа в примере. Как вы видите, остатки от деления слагаемых на 7 равны 1, 2, 3, 4, 5, 6. Например, «разберем» на составляющие число 7781:
7781 = 7777 + 4.
Аналогично можно «разобрать» другие числа примера.
Сумма наших «остатков» составляет 21:
1+2+3+4+5+6=21
Сумма остатков делится на 7 без остатка.

Переведем наш результат на обозначения теории чисел и сформулируем соответствующий вывод:
Если А≡В (mod M) и С≡D (mod M), то А+С≡В+D.
Иными словами, сравнения по одному и тому же модулю можно складывать.

Решение нашего примера в сравнении по модулю 7 запишем так:
8≡1, 79≡2, 780≡3, 7781≡4, 77782≡5, 777783≡6,
8+79+780+7781+77782+777783≡1+2+3+4+5+6≡21≡0 (mod 7)
Это означает, что сумма нашего числа делится на 7 без остатка.

Арифметические операции с остатками чисел по фиксированному модулю образуют модулярную (модульную) арифметику, применяемую не только в математике, но и в информатике и криптографии.

Попробуйте, не прибегая к калькулятору, решить следующие задачи:

Задача №176
Найдите остаток от деления на 7 числа:
7778*7779*7780*7781*7782*7783

Задача №177
Найдите последнюю цифру десятичной записи результата возведения 137 в сотую степень.

Задача №178
Какой цифрой оканчивается десятичная запись числа 333³³³?

Ответы к задачам №176, 177, 178 здесь: Арифметика остатков_2.

[1] Уи́льям Ро́уэн Га́мильтон (4 августа 1805 – 2 сентября 1865) – ирландский математик, механик-теоретик, физик-теоретик.