Задачи №176, 177, 178

После разбора «Арифметики остатков» и задачи №175, мы поставили перед собой вопрос решить без помощи калькулятора следующие задачи:
Задача №176
Каков будет остаток от деления на 7 числа:
7778*7779*7780*7781*7782*7783 ?

Задача №177
Найдите последнюю цифру десятичной записи результата возведения 137 в сотую степень.

Задача №178
Какой цифрой оканчивается десятичная запись числа 333³³³?

Начнем разбор решения с задачи №176.
Собственно говоря, эта задача очень похожа на задачу №175, но вместо суммы стоит произведение. Вопрос: обладает ли произведение таким же свойством, как и сумма при сравнении по модулю (см. Арифметика остатков).

Для примера рассмотрим произведение трех чисел: А, В, С.
Заменим А числом того же класса – А₁.
А₁ – это число, отличающееся от А на число, кратное 7, так как вполне очевидно, что модуль в рассматриваемой задаче – 7.
Значит,

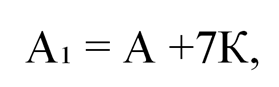
где К – некоторое целое число.
Следовательно,

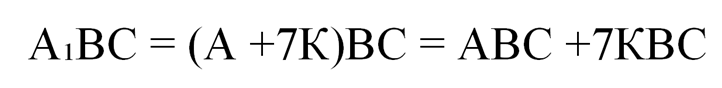
Отсюда следует, что АВС и А₁ВС отличаются на число, кратное 7, то есть принадлежат к одному классу.
Мы можем сделать четвертый вывод (первые три смотрите в «Арифметике остатков»): остаток от деления произведения нескольких чисел на модуль М не изменится, если один или даже несколько из сомножителей заменить числом того же класса.
В частности, мы можем заменить каждое число индексом его класса. В обозначениях теории числе это выглядит следующим образом:

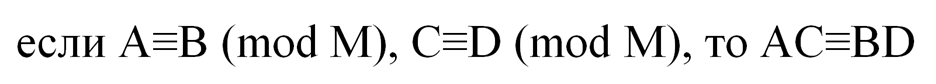
То есть сравнения по одному и тому же модулю можно перемножить!
Теперь мы легко можем решить поставленную перед нами задачу.
Зная, что остаток от деления, который мы должны определить, не изменится, если мы заменим все сомножители индексами их классов, напишем следующее выражение:
1*2*3*4*5*6≡720
720≡20≡6 (mod 7),
Это означает, что искомый остаток равен 6.

Примечание: рассуждения, сделанные при решении рассматриваемой задачи применимы и при решении задач с любым модулем М (М – натуральное число), отличным от 7. В таком случае, конечно, нам придется использовать таблицу, содержащую М столбцов.

Переходим к решению задачи №177
Найдите последнюю цифру десятичной записи результата возведения 137 в сотую степень.
Для решения задачи вспомним признак делимости на 10: Если последняя цифра в десятичной записи числа равна нулю, то это число делится на 10; кроме того, последняя цифра будет являться остатком от деления исходного числа на 10.
Воспользуемся арифметикой сравнения по модулю 10.
Внимательно изучим четвертый вывод «арифметики остатков», сделанный выше. Согласно ему, нам достаточно найти остаток от деления на 10 числа 7¹⁰⁰.
В арифметике остатков (арифметике сравнений) при сравнении по модулю 10 всякое натуральное число и его последняя цифра находятся в одном классе, поэтому, при возведении 7 (последняя цифра в 137) в степень нам необходимо отслеживать последнюю цифру степени.
При сравнении по модулю 10 это выглядит так:

• 7¹≡7 (mod 10)

Обратим внимание на последовательность:

• 7²≡9 (mod 10), так как мы делим 49 на 10;
• 7³≡7²*7≡9*7≡3 (mod 10);
• 7⁴≡7³*7≡3*7≡1 (mod 10);
• 7⁵≡7⁴*7≡1*7≡7 (mod 10).

Далее последовательность остатков (7, 9, 3, 1) будет повторяться.
Можно сделать вывод, что на 4-м, 8-м, 12-м, 16-м и т.д. месте, то есть на месте, кратном 4-м, в этой последовательности стоит цифра 1. Сотое место последовательности кратно 4-м. Следовательно, ответ на поставленный в задаче вопрос: 137¹⁰⁰ оканчивается на 1.

Найдем ответ к задаче №178
Какой цифрой оканчивается десятичная запись числа 333³³³?
Последовательность решения этой задачи аналогична решению задачи №177. Но в предыдущей задаче мы возводили в степень, кратную 10, а в данной задаче в степень 333.
Последние цифры степеней числа 333 образуют ряд:
3, 9, 7, 1, 3, 9, 7, 1 и т.д.
Например:

• 333¹=333, т.е. последняя цифра 3,
• 333²=…..9, так как 3*3 (последние цифры в числе) будет равно 9
• 333³=…….7, так как 3*3*3 (последние цифры в числе) будет равно 27.

Если продолжать далее, то 3*3*3*3=81. То есть 333 в четвертой степени будет оканчиваться на 1.
Как мы видим, повторяется группа из четырех цифр: 3, 9, 7, 1. После 1 снова идет 3, 9, 7.
При делении 333 на 4 в остатке мы получаем 1.
Значит 333≡1 (mod 4).
333 в степени 332 будет оканчиваться единицей.
Следовательно, 333³³³ оканчивается цифрой 3.

Попробуйте, не прибегая к калькулятору, решить следующие задачи:

Задача №179

Найдите последнюю цифру результата возведения числа 7 в степень 7⁷.

После возведения числа 7 в степень 7 отнимите от результата 4⁴⁴⁴. Найдите последнюю цифру результата.

Задача №180

Найдите остаток от деления 2¹⁰⁰⁰ на 7.

Задача №181

Сколько нулей в окончании десятичной записи числа 9⁹⁹⁹+1?

Задача №182

Делится ли 776⁷⁷⁶+777⁷⁷⁷+778⁷⁷⁸ на 3?

Ответы к задачам №179, 180, 181, 182 здесь: Арифметика остатков_3.