Задачи №179, 180, 181, 182, 183

Решим, используя правила «Арифметики остатков» (см. Арифметика остатков, Арифметика остатков_2) следующие задачи:

Задача №179
Найдите последнюю цифру результата возведения числа 7 в степень 7⁷.
После возведения числа 7 в степень 7 отнимите от результата 4⁴⁴⁴. Найдите последнюю цифру результата.

Задача №180
Найдите остаток от деления 2¹⁰⁰⁰ на 7.

Задача №181
Сколько нулей в окончании десятичной записи числа 9⁹⁹⁹+1?

Задача №182
Делится ли 776⁷⁷⁶+777⁷⁷⁷+778⁷⁷⁸ на 3?

Найдем ответ на первый вопрос задачи №179. Для этого обратимся к задаче №177, при решении которой мы нашли, что при возведении 7 в степень последовательность остатков (7, 9, 3, 1) повторяется через четыре. Необходимо узнать, какой остаток получится от деления 7⁷ на 4.

Представим 7⁷ как

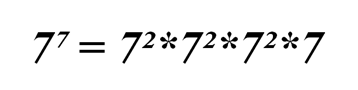
Так как

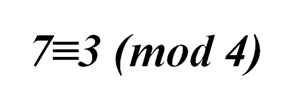
и

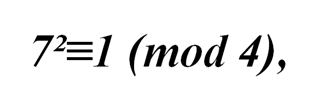
то

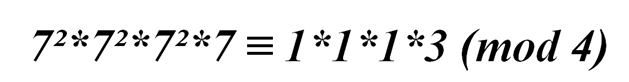
Значит, искомый остаток 7 в степени 7⁷ равен 3.

Далее найдем ответ на второй вопрос задачи. Для этого нам необходимо найти остаток числа 4⁴⁴⁴.
Если последовательно возводить 4 в степень, то последние цифры степеней четверки образуют ряд:

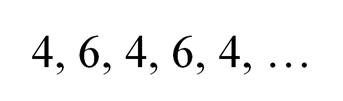
На нечетных местах у нас 4, а на четных – 6. Это означает, что последняя цифра числа 4⁴⁴⁴ – шестерка.
Остаток 7 в степени 7⁷ равен 3, а остаток 4⁴⁴⁴ – равен 6. При уменьшении 7 в степени 7⁷ на 4⁴⁴⁴ разность оканчивается на 7.

Задача №180: Найдите остаток от деления 2¹⁰⁰⁰ на 7.
Так как 2³=8≡1 (mod 7), то 2⁹⁹⁹≡1⁹⁹⁹≡1 (mod 7).
Значит, 2¹⁰⁰⁰≡2 (mod 7).
Искомый остаток — 2.

Для решения задачи №181 нам необходимо найти последние две цифры числа 9⁹⁹⁹+1. Две последние цифры произведения определяются двумя последними цифрами сомножителей. При возведении 9 в степень мы получаем ряд:

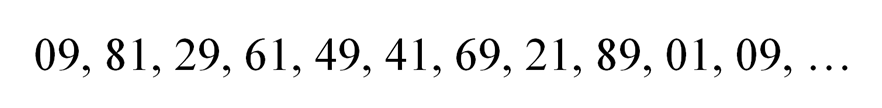
Далее последовательность будет повторяться. Период повторения – 10. Десять – модуль для решения нашей задачи.
Это означает, что последние две цифры числа 9⁹⁹⁹ такие же, как и у числа 9⁹, то есть – 89.
Значит, наше число 9⁹⁹⁹+1 оканчивается на 90.
Ответ на поставленный вопрос: в десятичной записи числа 9⁹⁹⁹+1 всего один ноль.

Перейдем к решению задачи №182. Делится ли 776⁷⁷⁶+777⁷⁷⁷+778⁷⁷⁸ на 3?
Вопрос, как вы понимаете, в возможности разделить число 776⁷⁷⁶+777⁷⁷⁷+778⁷⁷⁸ на 3 без остатка.
Для модуля 3

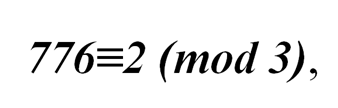
Значит,

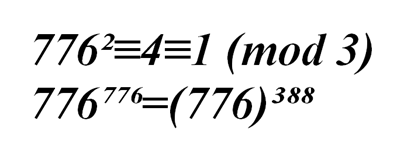
Следовательно,

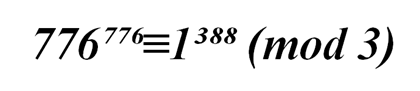
или

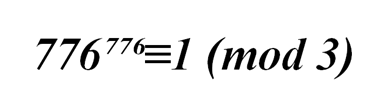
Найдем остаток для 777⁷⁷⁷. При делении 777 на 3 мы получаем нулевой остаток:

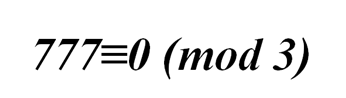
Значит,

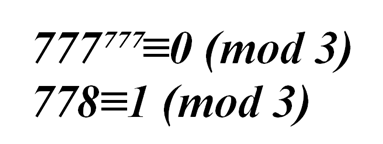
Отсюда

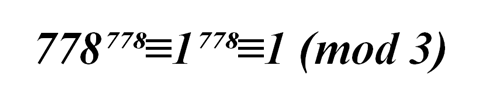
Мы получаем:

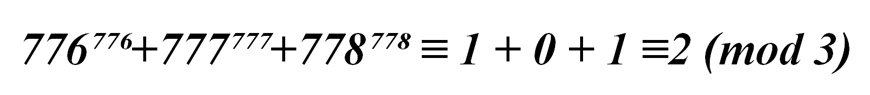
Значит, 776⁷⁷⁶+777⁷⁷⁷+778⁷⁷⁸ при делении на 3 дает остаток 2.

Модульная арифметика, как уже было указано, находит широкое применение. Она используется в теории чисел, в химии, информатике, криптографии и множестве других областей. Сравнение по модулю используется при определении ошибок ввода номеров банковских счетов. Построение регистрационных номеров в некоторых регистрационных системах строится, в том числе, и на применении принципов модульной арифметики.

Перейдем к другому типу задач – к задачам на «доказательство». При решении таких задач часто используется принцип, называемый «принцип Дирихле» в честь немецкого математика Иоганна Петера Густава Лежёна Дирихле[1].

В шуточной форме этот принцип можно сформулировать так: «Нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не более двух зайцев».

Решим, используя этот принцип такую задачу (задача №183):
Школьники классом из 30 человек отправились в лес собирать грибы. Один ученик собрал 13 грибов, а остальные ученики – меньше. Необходимо доказать, что по крайней мере 3 ученика собрали грибов поровну. При этом это может быть и полное отсутствие грибов, то есть ноль грибов.

Используя «принцип Дирихле» рассадим наших «зайцев» – учеников по «клеткам». В нашем случае «клетки» – это количество собранных грибов, включая ноль грибов.
«Клетка», в которой ученики с 0 грибов – нулевая.
«Клетка», в которой ученики с 1 грибом – первая.
Ряд «клеток» будет продолжаться до клетки под номером 13, куда попадет только один ученик, собравший 13 грибов.
Утверждение, данное в задаче, будем доказывать от противного. Предположим, что нет трех учеников с одинаковым количеством грибов. Значит, в каждую «клетку» попадет меньше трех учеников.
Мы знаем, что у нас «клетки» от 0 до 13. Всего 14 клеток. При этом в «клетке» 13 всего один ученик.
В таком случае, в наших «клетках» поместится не более
13*2 + 1 = 27.

Всего в классе 30 человек. Значит, мы получили противоречие.
Следовательно, утверждение задачи верно и не менее трех учеников собрали равное количество грибов.

Решите задачу №183 при следующих условиях (задача №184): В лес отправился 41 ученик. Остальные условия задачи такие же, как в задаче №183.
Необходимо доказать, что найдутся четверо, собравших одинаковое количество грибов.

Ответ к задаче №184 здесь: Принцип Дирихле

[1] Ио́ганн Пе́тер Гу́став Лежён Дирихле́ (13 февраля 1805 – 5 мая 1859) – немецкий математик, внесший вклад в развитие математического анализа, теории функций, теорию чисел.