Задачи №186, 187, 188, 189, 190, 191, 192

Разбирая «принцип Дирихле», мы должны были решить следующие задачи:

Задача №186.
В строку выписано 5 натуральных чисел:

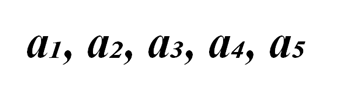
Докажите, что либо одно из них делится на 5, либо сумма нескольких рядом стоящих чисел делится на 5.

Задача №187.
В строку вписано n чисел. Докажите, что либо одно из них делится на n, либо сумма нескольких рядом стоящих чисел делится на n.

Задача №188.
Встретились два человека. Назовем одного – Оптимист, а второго – Пессимист.
Перед ними прямоугольный двор размером 150 на 110 метров, загроможденный строениями: 10 складов 20*20 метров, 4 цеха 40*10 метров, круглое бензохранилище с радиусом 10 метров.
Оптимист утверждает, что сможет на данном дворе разбить клумбу радиусом 5 метров.
Пессимист уверен, что найти место под такую клумбу на территории двора невозможно.
Кто из них прав?
Примечание: отбросим условности в виде проездов, проходов, дверей и ворот, так как мы решаем чисто теоретическую задачу.

Задачи №186 и №187 решаются довольно просто.

Вначале решим задачу №186. Для этого рассмотрим пять чисел, получаемых из данного нам в задаче ряда:

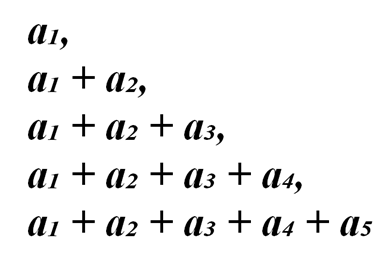
По условиям задачи мы должны доказать, что либо одно из них делится на 5, либо сумма нескольких рядом стоящих чисел делится на 5.
Если одно из них делится на 5, то утверждение что либо одно из них делится на 5, либо сумма нескольких рядом стоящих чисел делится на 5, справедливо. В противном случае указанные числа дают в остатке какие-либо из четырех чисел:

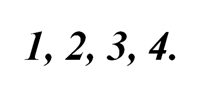
Исходя из принципа Дирихле, остатки по крайней мере двух из указанных чисел совпадают, значит, разность их делится на 5.
Но получаемая разность – одно из чисел, данных в задаче, или сумма нескольких из них, стоящих рядом. Следовательно, утверждение доказано.

Решение задачи №187 повторяет решение задачи №186, за тем лишь исключением, что мы заменяем число 5 на n.

Мы получаем теорему, схожую с теоремой, полученной при решении задачи №185 (см. Принцип Дирихле): Пусть n – натуральное число. Из любых n+1 натуральных чисел можно выбрать два, сумма которых делится на n.
Обратите внимание: не «все», а «можно выбрать».

Перейдем к задаче №188:
Повторим условия: Встретились два человека. Назовем одного – Оптимист, а второго – Пессимист.
Перед ними прямоугольный двор размером 150 на 110 метров, загроможденный строениями: 10 складов 20*20 метров, 4 цеха 40*10 метров, круглое бензохранилище с радиусом 10 метров.
Оптимист утверждает, что сможет на данном дворе разбить клумбу радиусом 5 метров.
Пессимист уверен, что найти место под такую клумбу на территории двора невозможно.
Кто из них прав?
Примечание: отбросим условности в виде проездов, проходов, дверей и ворот, так как мы решаем чисто теоретическую задачу.

Перед тем, как её решить, отвлечемся и представим себе небольшой луг и козу, пасущуюся на этом лугу. Для того, чтобы коза не убежала в лес, её привязывают колышку и она съедает траву в доступном её пространстве. Как вы понимаете, это пространство ограничено длиной веревки, которой коза привязана к колышку, и представляет собой круг.

«Привяжем» козу иначе. Для этого вобьем в землю два колышка и между ними натянем веревку. Привязь козы прикрепим к веревке, натянутой между колышками.
Пространство, доступное козе, изменится. Теперь это будет фигура, представленная на рисунке 1.

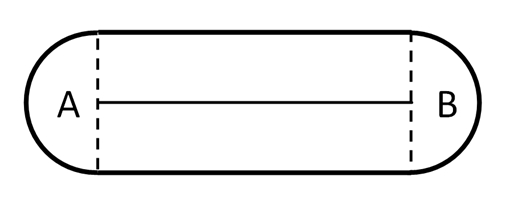
В нашем случае отрезок АВ – это натянутая между колышками веревка.

Отпустим нашу козу восвояси, так как далее её «эксплуатация» в качестве наглядного материала приведет нас к множеству условностей, таких как длина шеи козы, натяжение веревки, к которой она привязана и т.д. Иди себе, пасись.

Мы же обратимся к козе «математической», для которой не нужно делать дополнительных допущений и предположений. Обозначать мы будем эту козу точкой, «привяжем» её веревкой-отрезком, а «съедать траву» она будет на точно обозначенных линиями фигурах. А вот как эти фигуры образуются, мы сейчас и разберемся.

Расстояние от отрезка АВ до границы фигуры, представленной на рисунке 1, ограничено отрезком постоянной длины – веревкой, которой привязана наша математическая коза.
Обозначим точкой М нашу козу и представим, что она находится на границе нашей «площадки» (рисунок 2):

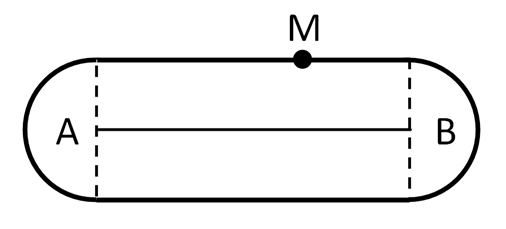
Расстоянием от точки М до отрезка АВ называется наименьшее из расстояний от точки М до точек отрезка АБ (назовем это – определение 1).

Представим себе, что мы решили увеличить площадь, к которой у козы будет доступ. Для этого мы забили два дополнительных колышка: С и D. Между С и D мы натянули дополнительную веревку, равную по длине АВ и перпендикулярно АВ, а козе добавили дополнительную привязь, равную первой привязи. Обычной козе пришлось бы туго, но наша коза математическая, а потому спокойно отнеслась к этим ограничениям.

На рисунке 3 изображена фигура, которую мы получили.

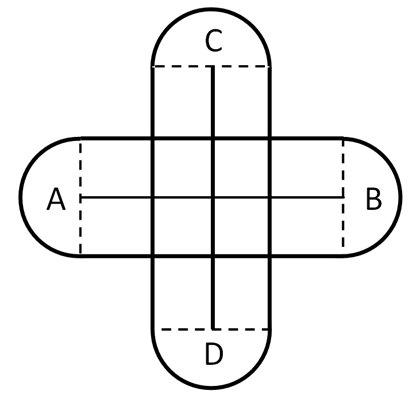
Как вы думаете, к какому участку на полученной нами фигуре имеет доступ наша коза? Для решения этого вопроса необходимо четко представлять те ограничения, которые мы сделали, «привязав» козу двумя одинаковыми привязями к двум разным отрезкам АВ и СD.

Теперь, вместо площадки, ограниченной фигурой на рисунке 1 или аналогичной перпендикулярной ей площадке с отрезком СD (если привязать только одной привязью к отрезку СD), мы ограничим нашу козу квадратом, изображенным в виде заштрихованной поверхности на рисунке 4.

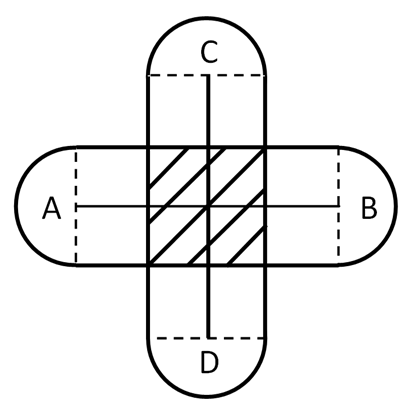
Т.е., изменяя количество «колышков» с веревкой (АВ, СD, EF и т.д.) и соответствующее количество привязей, мы можем «заставить» нашу математическую козу «съедать траву» на участке, изображающем ту или иную фигуру. С живой козой такое уж точно бы не получилось.

Попробуйте, к примеру, ограничить козу параллелограммом (задача №189) или шестиугольником (задача №190). То есть с помощью минимально необходимого количества «колышков» (с веревками между ними) и привязей изобразите «ограничивающую» козу фигуру.

Рассуждаем далее. Обозначим фигуру, получаемую при наших экспериментах с «козой» через Ф.
Тогда мы можем сказать, что окрестность радиуса R фигуры Ф – это множество всех тех точек, расстояние от которых до фигуры Ф не превосходит R (определение 2).
Расстояние от точки до фигуры есть обобщение понятия «расстояние от точки до отрезка» (см. выше определение 1).
Тогда расстояние от точки М до фигуры Ф – наименьшее из расстояний (если таковое существует) от точки М до точек фигуры Ф (определение 3).
Это означает, что если наша фигура Ф – отрезок, то мы получим совпадение для определений 3 и 1.

Предположим, что мы натянули веревки по прямоугольнику и коза ходит на привязи, ограниченной этим прямоугольником и меньшей, чем половина короткой стороны прямоугольника. Тогда окрестность «доступной» нашей козе фигуры будет изображаться в виде заштрихованной части на рисунке 5.

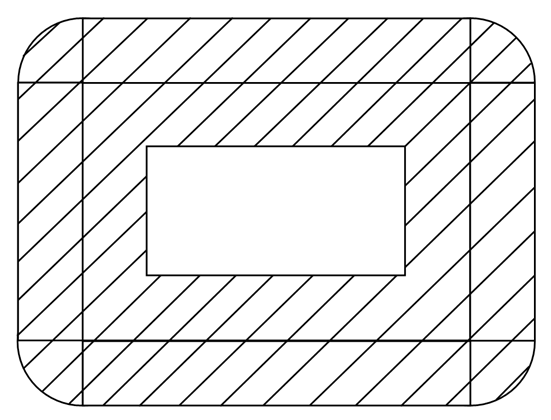
Попробуйте изобразить окрестности радиуса 1 следующих фигур (задача №191):

• креста (пересечения двух равных отрезков длиной 4);
• окружности (радиус окружности – 2);
• равностороннего треугольника (медиана равна 4);

Вот вам и следующая задача (задача №192): Как найти площадь окрестности радиуса R выпуклого многоугольника площадью S и периметром P?

Наша «математическая коза на привязи» дает общее представление о построении фигур при наличии определенных ограничений.

Вернемся к задаче №188 и выясним, кто же прав – Оптимист или Пессимист в вопросе разбивки клумбы на дворе, занятом множеством построек.
Предполагаемая клумба должна иметь радиус 5 метров (см. условия задачи №188). Значит, центр клумбы должен находиться на расстоянии не менее 5 метров от строений и забора, которым, как мы полагаем, обнесен наш прямоугольный участок. Ту часть двора, где центр (!) клумбы не может располагаться, назовем «запретной зоной».
Какова же площадь нашей «запретной зоны»? Для ответа на этот вопрос необходимо найти площадь окрестностей радиуса 5 метров строений во дворе и площадь окрестности забора, пересеченной с двором. Что такое «окрестность фигуры» – смотри выше.
Если вы решили задачу №192, то вы легко найдете площадь запретной зоны. Если нет, то прочитайте решение к этой задаче (см. следующую статью).
Площадь окрестности запретной зоны забора равна 2500 квадратных метров. Она рассчитывается как разность между площадью нашего двора и площадью прямоугольника, подобного по форме двору, но уменьшенного с каждой стороны на 5 метров — на радиус клумбы. То, что находится за пределами двора, нас не интересует.
Запретная зона бензохранилища – это круг, радиусом 15, в который входит само бензохранилище, радиусом 10 метров, плюс радиус клумбы – 5 метров. Указанная запретная зона составляет порядка 706,5 квадратных метров. Нам такая точность не важна, а потому мы возьмем на указанную запретную зону 710 квадратных метров.
Для складов и цехов площадь запретной зоны рассчитаем по формуле, полученной при решении задачи №192.
Для склада 20*20 метров такая площадь будет составлять 878,5 квадратных метров. Округлим её до 900 квадратных метров.
Для цеха 40*10 метров запретная зона будет составлять 978,5 квадратных метров. Округлим до 1000 квадратных метров.
Как вы понимаете, все наши запретные зоны находятся внутри одного нашего двора. Площадь всей запретной зоны не превосходит суммы площадей запретных зон, порождаемых забором и строениями. Она будет даже меньше, если некоторые из строений расположены менее чем в 10 метрах друг от друга или от забора.
Значит, площадь запретной зоны меньше, чем
2500 + 710 + 10*900 + 4*1000 = 16210 м²
Площадь же всего нашего двора – 16500 м².
Остается участок площадью более 290 м², в каждой точке которого можно расположить центр клумбы.
Оптимист оказался прав!

Для решения задачи №188 мы использовали вариант принципа Дирихле, который, применимо к условиям задачи, звучит так: если сумма всех площадей фигур внутри двора меньше площади двора, то найдется точка двора, не принадлежащая ни одной из фигур.
В нашем случае фигурами были не забор, склады, цеха, бензохранилище, а порождаемые ими «запретные зоны».

Решение задач №189, 190, 191, 192 здесь: Коза на привязи_2.