Задачи №189, 190, 191, 192, 193, 194, 195, 196

В теме «Коза на привязи» мы разбирали способы ограничить площадку для выпаса некой условной козы. Для удобства и ухода от массы условностей, для наших опытов использовали козу «математическую».
Как ограничить козу квадратным полем смотрите в статье «Коза на привязи». А вот как ограничить нашу козу параллелограммом (задача №189)?
Сложностей, как вы понимаете, в этом вопросе нет. Для получения квадратного поля для козы мы использовали фигуру, изображенную на рисунке 1.

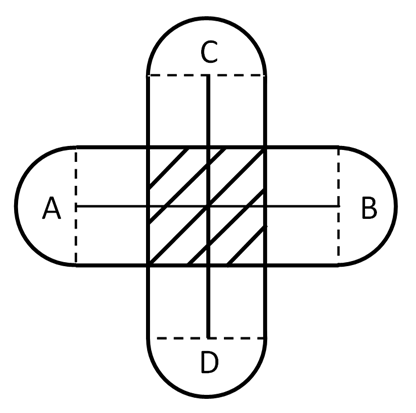
Соответственно, для получения параллелограмма мы просто переставим колышки С и D, расположив отрезок СD к отрезку АВ под углом, отличным от прямого. Например, как изображено на рисунке 2.

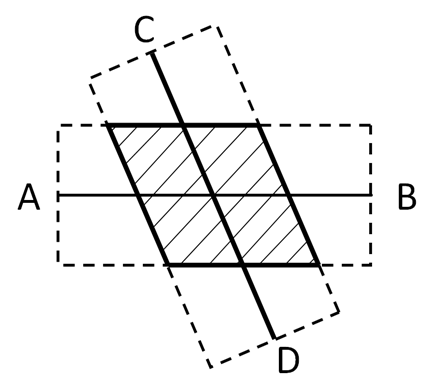
Поле, ограничивающее нашу козу, выделено и заштриховано.

Перед тем, как ограничить козу шестиугольником (задача №190), мы решим другую задачу и ограничим её треугольником.
Для этого к нашему параллелограмму добавим еще два колышка: E и F. А к отрезку (веревке) EF будет прикреплена дополнительная привязь (см. рисунок 3).

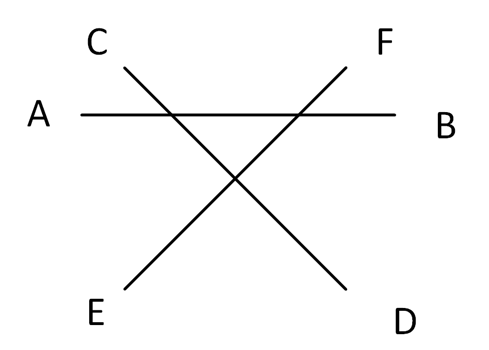
Пересечение наших отрезков образует треугольник, за пределы которого нашей «козе», привязанной равной длины привязями, никак не выбраться.

Теперь ограничим козу шестиугольником (задача №190). Для этого нам понадобятся все те же три отрезка (веревки), к которым и будут прикреплены три привязи, но расположим мы их иначе (рисунок 4).

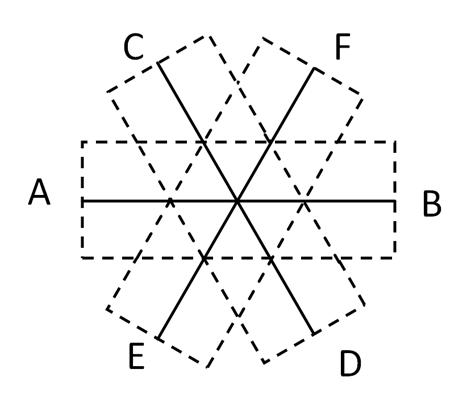
Теперь мы можем выделить наш шестиугольник, ограничивающий козу (рисунок 5).

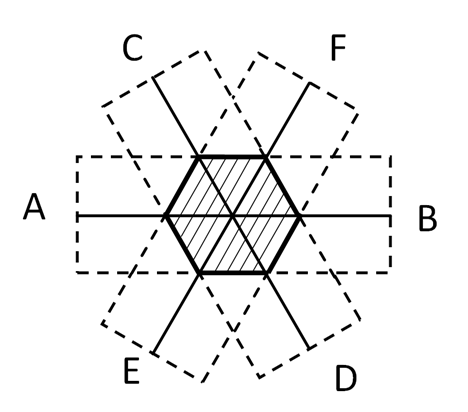
Удобнее даже сначала нарисовать правильный шестиугольник, а затем провести через его центр отрезки-веревки, к которым прикрепить соответствующей длины привязи, для получения необходимых граней.

Далее нам необходимо было изобразить окрестности радиуса 1 следующих фигур (задача №191):

• креста (пересечения двух равных отрезков длиной 4);
• окружности (радиус окружности – 2);
• равностороннего треугольника (медиана равна 4);

Окрестность креста изобразим на примере наших отрезков АВ и СD, с помощью которых мы предоставили козе квадратный участок.
Отличие в том, что в данном случае мы рисуем именно окрестность фигуры, полученной пересечением отрезков (рисунок 6). Можно нарисовать с указанием размеров.

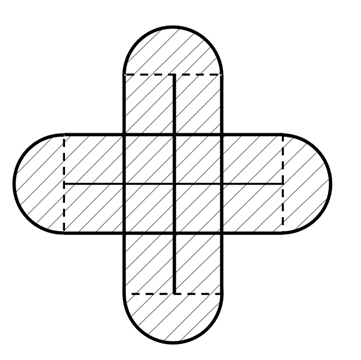
Окрестность радиуса окружности в нашем случае – кольцо.

Окрестность радиуса 1 для равностороннего треугольника с медианой 4 будет выглядеть следующим образом (нарисовано исключительно для наглядного представления, а потому – без размеров):

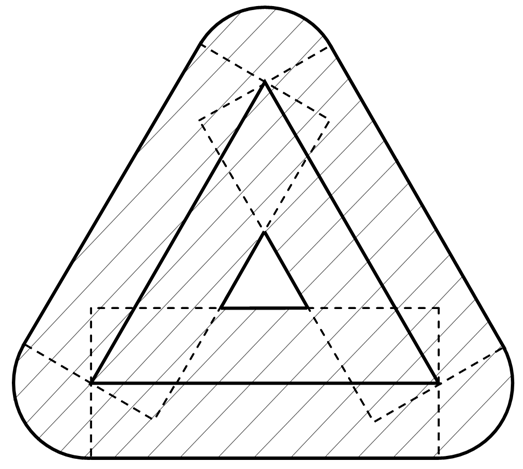
Перейдем к задаче №192: Как найти площадь окрестности радиуса R выпуклого многоугольника площадью S и периметром P?

Для начала выясним, из каких частей состоит окрестность выпуклого многоугольника. Это:

• сам многоугольник;
• прямоугольники, основания которых – стороны многоугольника, а высоты равны R;
• сектора радиуса R с центрами в вершинах многоугольника.

Сумма углов выпуклого многоугольника равна 180°(n – 2), где n – число сторон многоугольника. Следовательно, объединение секторов радиуса R с центрами в вершинах многоугольника составляет полный круг, площадь которого равна πR².
Отсюда вывод: площадь окрестности выпуклого многоугольника равна

В качестве дополнительной задачи (задача №193): Предоставьте козе для выпаса сектор, используя не более пяти колышков.

Используя «круги Эйлера», «принцип Дирихле», ограничивая условную «козу» привязью, мы решаем задачи, связанные с множествами. При этом мы не обходимся и без Булевой алгебры.

Отличительной особенностью решенных задач является наличие определенных (выраженных) ограничений. Например, то или иное пересечение множеств с образованием подмножеств, при решении с помощью кругов Эйлера, или длина условной привязи при решении задач с «козой», или наличие ограниченного количества клеток (ячеек) при построении доказательств с помощью принципа Дирихле.

А что, если у нас нет точной информации по всем множествам, а есть только информация по части из них?
Решите, например, такие задачи:
Задача №194
Известно, что в урне не все шары белые. Верно ли, что там есть красный шар?

Задача №195
Известно, что в урне не все шары одного цвета. Верно ли, что в урне есть хотя бы один цветной шар?

Задача №196
В урне 10 белых, 8 синих, 11 зеленых шаров. Сколько надо вынуть шаров, чтобы наверняка:

• попался белый шар,
• попались шары всех трех цветов?

Решение задач №193, 194, 195, 196 здесь: Построение отрицаний.