Задачи №184, 185, 186, 187, 188

Мы должны решить следующую задачу, используя «принцип Дирихле» (см. задачу №183 в «Арифметика остатков_3»):
Школьники в количестве 41 человек отправились в лес собирать грибы. Один ученик собрал 13 грибов, а остальные ученики – меньше. Необходимо доказать, что по крайней мере 4 ученика собрали грибов поровну. При этом это может быть и полное отсутствие грибов, то есть ноль грибов.

Решение этой задачи абсолютно аналогично решению задачи №183.
Используя «принцип Дирихле» мы рассадим наших «зайцев» – учеников по «клеткам». В нашем случае «клетки» – это количество собранных грибов, включая ноль грибов.
«Клетка», в которой ученики с 0 грибов – нулевая.
«Клетка», в которой ученики с 1 грибом – первая.
Ряд «клеток» будет продолжаться до клетки под номером 13, куда попадет только один ученик, собравший 13 грибов.

Утверждение, данное в задаче, будем доказывать от противного. Предположим, что нет четырех учеников с одинаковым количеством грибов. Значит, в каждую «клетку» попадет меньше четырех учеников.
Мы знаем, что у нас «клетки» от 0 до 13. Всего 14 клеток. При этом в «клетке» 13 всего один ученик.
В таком случае, в наших «клетках» поместится не более
13*3 + 1 = 40.

Всего за грибами отправился 41 человек. Значит, мы получили противоречие.
Следовательно, утверждение задачи верно и не менее четырех учеников собрали равное количество грибов.

Задачи №183 и №184 очень просты и предназначены для общего понимания работы «принципа Дирихле».

Вот задача несколько сложнее (задача №185):
Докажите, что из любых 12 натуральных чисел можно выбрать два, разность которых делится на 11.

Эта задача решается также просто, как и обе предыдущие задачи. Но мы должны помнить, что остаток — это целое число, «оставшееся» после деления одного целого числа на другое для получения целочисленного частного. То есть деление остатка приводит к получению дробной части (см. Арифметика остатков).

При делении на 11 мы получаем один из 11 остатков: 0, 1, 2, 3, …, 10. Мы заполнили 11 «клеток», но нам дано 12 чисел, а это значит, что остатки от деления на 11 у каких-то двух их них совпадают.
Следовательно, разность этих двух чисел делится на 11.

При решении мы использовали и «принцип Дирихле» и знания, полученные из темы «Арифметика остатков».

Задача №185 является частным случаем следующей теоремы:
Пусть n – натуральное число. Из любых n+1 натуральных чисел можно выбрать два, разность которых делится на n.

Действительно, при делении на n получается один из n остатков: 0, 1, 2, 3, …, n-1. Так как нам дано n чисел, и по принципу Дирихле остатки от деления на n у каких-то двух из них совпадают, то разность этих двух чисел делится на n.

Попробуйте в качестве тренировки решить следующие задачи:

Задача №186.
В строку выписано 5 натуральных чисел:

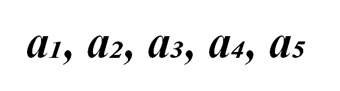
Докажите, что либо одно из них делится на 5, либо сумма нескольких рядом стоящих чисел делится на 5.

Задача №187.
В строку вписано n чисел. Докажите, что либо одно из них делится на n, либо сумма нескольких рядом стоящих чисел делится на n.

А также решите задачку чуть сложнее (задача №188):
Встретились два человека. Назовем одного – Оптимист, а второго – Пессимист.
Перед ними прямоугольный двор размером 150 на 110 метров, загроможденный строениями: 10 складов 20*20 метров, 4 цеха 40*10 метров, круглое бензохранилище с радиусом 10 метров.
Оптимист утверждает, что сможет на данном дворе разбить клумбу радиусом 5 метров.
Пессимист уверен, что найти место под такую клумбу на территории двора невозможно.
Кто из них прав?
Примечание: отбросим условности в виде проездов, проходов, дверей и ворот, так как мы решаем чисто теоретическую задачу.

Решение задач №186, 187, 188 здесь: Коза на привязи.