Задачи №199, 200, 201

Для начала решите очень простую задачу.
Задача №199:
Имеется 26 одинаковых по виду и по достоинству новеньких монет. Но среди них одна фальшивая. Фальшивая монетка легче остальных. Есть чашечные весы (весы без стрелки и без гирь).
Сколько вам потребуется взвешиваний, чтобы найти фальшивую монету?

Если вы решали задачу про орехи (задача №26: «Орехи. 1 из 9. 1 из 27. 1 из Х»), то с легко решите и эту задачу. Очевидно, что нам потребуется 3 взвешивания (см. ответ к вопросу «1 из Х»).
Сначала мы кладем на каждую чашу весов по девять монет. У нас остается еще восемь.
Если чаши уравновесились, то фальшивая монета в оставшейся части.
Если не уравновесились, то фальшивая монета там, где чаша с монетами оказалась легче.
Берем еще по три монеты, и у нас остается 3 монеты (если фальшивая монета в чаше весов) или 2 монеты (если фальшивая монета среди еще не взвешенных монет).
Мы снова получим либо равновесие, либо перевешивание одной из чаш. Тогда фальшивая монета будет на чаше с монетами, которая оказалась легче. Или монета окажется среди двух оставшихся.
Останется только положить на весы по одной монете.
Если мы брали для взвешивания монеты с чаши весов, то либо весы покажут нам эту монету, либо она будет третьей, которая не попала на весы.
Если же нам пришлось взвесить «остаток» — наши две монеты, которые до этого на весях не побывали, то весы в любом случае покажут фальшивку.
Проводя каждое из взвешиваний, мы уменьшаем количество возможных вариантов нахождения фальшивой монеты. Весы, в свою очередь, отвечают нам на вопрос о возможном нахождении на них фальшивой монеты вариантами:

• перевешивание одной из чаш;
• равновесие.

Если перевести в вариант «вопрос-ответ», то мы получим логичную схему:
Вопрос: У сравниваемых монет одинаковый вес?
Ответ: Да/Нет.

Если ответ «Да», то мы выбираем группу монет с интересующим нас отклонением для последующего испытания.
При ответе «Нет», испытанию подвергаются ранее не задействованные монет.

После каждой серии таких вопросов мы уменьшаем количество монет, задействованных в испытании, и проводим новое испытание с тем же вопросом.

Примечание: На самом деле схема несколько сложнее, так как помимо ответа «Да/Нет», должна присутствовать дополнительная информация к ответу «Да»: указание на группу монет с интересующим нас отклонением от заданного норматива. Это можно решить дополнительным вопросом, обозначив наши чаши «левая» и «правая» (или №1 и №2). Выглядеть это может так:

Вопрос: Монеты на левой чаше весов легче?
Ответ: Да/Нет.

Если ответ «Нет», то легче, разумеется, монеты на правой чаше весов.

Немного переформулировав вопросы и исключив сам процесс деления на группы, мы можем очень упрощенно изобразить нашу схему так:

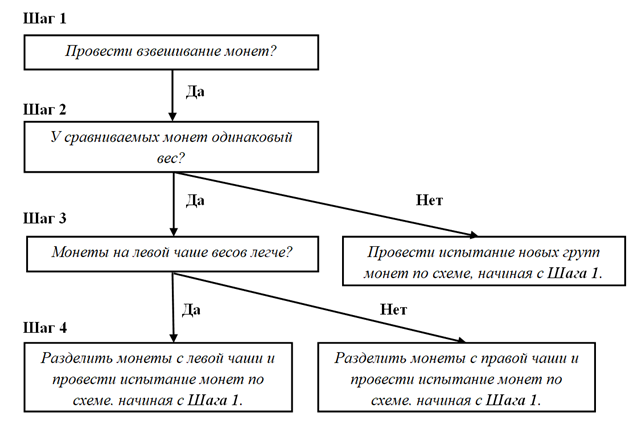
Такая схема понятна нам, так как многие действия мы делаем изначально понимая требования к ним, но дополнительно эти требования не описывая. Но как программа такая схема работать не будет, в силу того, что для автоматизированной обработки схема должна содержать четкое описание действий. Или, как вариант, отсылку к порядку действий в том или ином случае. Например, для шага 1 должно быть указано, какие монеты («группы объектов») должны быть выбраны для сравнения. То есть должны быть указаны их характеристики, по которым они будут отобраны для взвешивания, или порядковые номера «групп» монет.
Для шага 2 необходимо сразу задать «норматив», по которому проводится сравнение. Для нас это «одинаковый вес» сравниваемых групп монет.

Важным является то, что четко прописав алгоритм наших действий, мы можем получить простейшую программу, основанную на принципе однозначных ответов: «Да» и «Нет».
Заменив «Да» на 1, а «Нет» на 0, мы придем к двоичному коду, лежащему в основе программирования.
Именно поэтому мы, если хотим составить программу, не можем задать вопрос: «левая или правая чаша весов легче?». Наш вопрос должен приводить к ответу «Да/Нет» или «1/0».

Решите другую задачу (задача №200):
Перед вами две группы монет по три монеты в каждой. Монеты одинаковы по виду и достоинству.
Известно, что в каждой группе одна из трех монет фальшивая, имеющая меньший вес, чем настоящая.
Есть чашечные весы (весы без стрелки и без гирь).
Сколько вам потребуется взвешиваний, чтобы найти фальшивую монету?

Ответ для данной задачи очевиден: потребуется всего два взвешивания. Сначала проводим взвешивание первой группы, а затем второй группы.

Вот более сложная задача (задача №201):
Вам необходимо выяснить у вашего собеседника некий номер, состоящий из пяти цифр.
Вы можете задавать вопросы вашему собеседнику, на которые он отвечает «Да» или «Нет».
Какой способ вы должны выбрать, чтобы количество вопросов было минимальным? И сколько минимально вам потребуется вопросов для выяснения загаданного номера?

Ответ к задаче №201 здесь: Комбинаторика.