Задачи №208, 209, 210, 211, 212

Нам необходимо решить две задачи:

Задача №208
В коробке лежат 5 зеленых, 12 белых и 9 черных кубиков.
Какова вероятность того, что:

• будет вынут белый кубик;
• будет вынут зеленый кубик;
• будет вынут черный кубик;
• будет вынут цветной (не белый) кубик?

Задача №209
В коробке лежат 3 синих и 4 белых кубика.
Вы вынимаете один кубик, затем кладете его обратно и перемешиваете содержимое. После этого вы снова вынимаете из коробки первый попавшийся кубик.
Возможно следующее из трех сочетаний: оба кубика синие, оба кубика белые, кубики различны по цвету.
Какова вероятность каждого из сочетаний?

Так как исходы вынимания кубиков равновозможны, то при решении мы будем использовать формулу определения вероятности событий, приведенную здесь: События и вероятности.

Для ответа на вопросы задачи №208 найдем количество возможных исходов вынимания кубиков. Так как по условиям задачи нам необходимо вынуть только один кубик, то достаточно сложить количество кубиков каждого цвета:

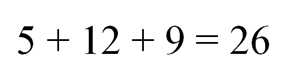
То есть равновозможны 26 различных исходов вынимания кубика того или иного цвета.

Далее найдем вероятности вынимания кубиков, цвета которых указаны в вопросах задачи.

Для первого вопроса (белый кубик) вероятность равна:
12 белых кубиков / 26 равновозможных исходов при вынимании кубика.
Вероятность того, что будет вынут белый кубик, равна:

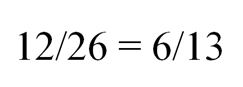
Аналогично мы найдем ответ и на последующие вопросы задачи.
Вероятность того, что будет вынут зеленый кубик, равна 5/26.
Вероятность того, что будет вынут черный кубик, равна 9/26.
Вероятность того, что будет вынут цветной кубик, равна:

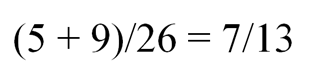
Несколько сложнее (но не сильно) решается задача №209 (условия см. выше).
Для наглядности составим таблицу, в которой парами букв покажем возможные вариаций цвета вынимаемых кубиков (рис. 1). Крайний левый столбец таблицы будет показывать цвет кубика при первом вынимании, а верхняя строка – цвет кубика при втором вынимании. Первая буква в сочетании будет отражать цвет кубика при первом вынимании, а вторая – при втором вынимании.
Всего у нас семь кубиков. Значит, возможны семь исходов при первом вынимании и семь исходов при втором вынимании (мы же возвращаем кубик обратно после первого вынимания). Цифра обозначает порядковый номер исхода.

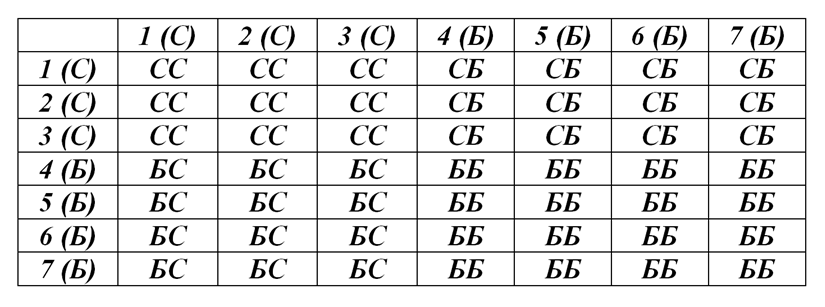
То есть, у нас получилось:
7 равновозможных исходов при первом вынимании кубика;
7 равновозможных исходов при втором вынимании.
Итого: 7*7 = 49 равновозможных исхода вынимания кубиков.

Можно не заглядывая в таблицу найти количество исходов, когда в наших руках дважды окажется синий кубик:
3 исхода (у нас всего три кубика синего цвета) при первом вынимании кубика;
3 исхода при втором вынимании.
Итого: 3*3 = 9 возможных исходов вынимания кубиков синего цвета.
Вероятность того, что синий кубик окажется в наших руках после каждого из выниманий, равна:

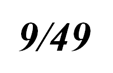
Аналогично найдем ответы для последующих вопросов задачи: пересчитав возможные варианты появления требуемого результата по таблице или перемножив варианты исхода:

Дважды вынуть белый кубик:
4 исхода при первом вынимании * 4 исхода при втором вынимании.
Вероятность события «белый и белый» равна:

Для того, чтобы найти исходы, при которых будут вынуты кубики различных цветов, необходимо сложить исходы БС и СБ:
БС: 4 исхода Б при первом вынимании * 3 исхода С при втором вынимании.
СБ: 3 исхода С при первом вынимании * 4 исхода Б при втором вынимании.

Значит, вероятность события «два кубика разного цвета» равна:

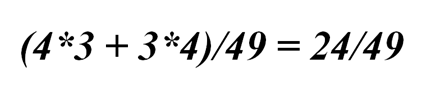
Вы легко сможете решить задачу №210:
У вас такое же количество кубиков и такие же условия вынимания кубиков, что и в задаче №209.
Необходимо найти вероятность вынуть:

• вынуть по крайней мере один синий кубик;
• вынуть хотя бы один белый кубик;
• вынуть первым синий кубик;
• вынуть белый кубик последним.

Попробуйте решить следующие задачи.

Задача №211:
У вас две классических игральных кости с шестью гранями и числами на гранях от 1 до 6.
При подбрасывании любая из шести граней может оказаться верхней.
Вы подбрасываете обе игральные кости.
Необходимо найти вероятность того, что сумма очков (чисел) на верхних гранях:

• меньше 9;
• больше 7;
• делится на 3;
• четна.

Задача №212:
Вы играете с равным вам по силам противником игру. Например, в шахматы. Или, допустим, в теннис.
Что вероятнее: выиграть у равного вам по силам противника три партии из четырех или пять партий из восьми?

Ответы к задачам №210, 211, 212 здесь: События и вероятности_3.