Задачи №207, 208, 209

Французский писатель Антуан Гомбо[1], будучи математиком-любителем, на одном из частных вечеров предложил решить такую задачу (задача №207):
Два игрока поочередно подбрасывают монету. Первый игрок поставил на гербы (орлы), второй – на решки. Выигрывает тот, кто первым наберет три выигрышных для него случая падения монеты. Но игра прервана тогда, когда у первого игрока уже имелось «на счету» два герба, а у второго – одна решка.
Игроки договорились разделить ставку пропорционально шансам каждого на выигрыш.
Как должна быть разделена ставка?

Примечание: еще одну задачу Антуана Гомбо можно посмотреть здесь: Задача шевалье де Мере.

Решить задачу взялись Блез Паскаль[2] и Пьер Ферма (Пьер де Ферма)[3] — одни из основоположников теории вероятностей.
Именно первые попытки математического анализа азартных игр лежали в основе развития теории вероятностей[4]. Вероятностные закономерности, возникающие при бросании игральных костей, изучали Паскаль, Ферма, Гюйгенс[5], Бернулли[6]. Паскаль называл это – «Математика случая».

Задолго до перечисленных выше ученых вопрос вероятности получения выигрыша изучал Джероламо Кардано[7]. Работа Кардано «Книга об игре в кости» была написана еще в 1526 году, но была опубликована после его смерти – в 1663 году. «Книга об игре в кости» – один из первых серьёзных трудов по комбинаторике и теории вероятностей. В этой же работе Кардано сделал очень существенное замечание: реальное количество исследуемых событий может при небольшом числе игр сильно отличаться от теоретического, но чем больше игр в серии, тем доля этого различия меньше. Впоследствии этот принцип был развит до «Закона больших чисел» – принципа, описывающего результат выполнения одного и того же эксперимента много раз.

Если выигрыш мы назовем «благоприятным исходом», то основную формулу классической теории вероятностей можно изложить так:

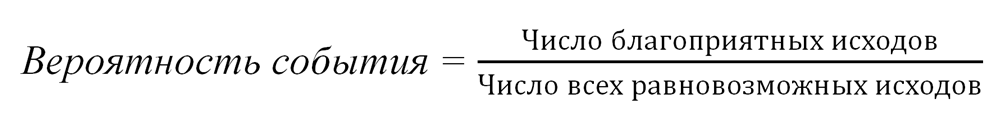
Эта формула подходит для случаев, когда исходы опыта равновозможны и надо только вычислить вероятность «благоприятного» исхода.

Перейдем непосредственно к решению задачи, предложенной Антуаном Гомбо.
Для её решения «проведем» вспомогательный опыт, состоящий в двукратном бросании монеты. Саму монету мы подбрасывать не будем, но запишем все возможные результаты, обозначив «герб» буквой Г, а «решку» буквой Р.
Равновозможны четыре исхода:
ГР – при первом бросании выпадает герб, а при втором – решка;
ГГ
РГ
РР

Первые три случая однозначно приводят к победе первого игрока, уже имеющего на своем счету два выпавших герба.
Второй игрок выигрывает только при получении четвертого исхода бросков.
Значит, шансы игроков на выигрыш относятся как 3 к 1. В таком соотношении и следует разделить ставку между игроками.

Попробуйте решить аналогичные задачи:
Задача №208
В коробке лежат 5 зеленых, 12 белых и 9 черных кубиков.
Какова вероятность того, что:

• будет вынут белый кубик;
• будет вынут зеленый кубик;
• будет вынут черный кубик;
• будет вынут цветной (не белый) кубик?

Задача №209
В коробке лежат 3 синих и 4 белых кубика.
Вы вынимаете один кубик, затем кладете его обратно и перемешиваете содержимое. После этого вы снова вынимаете из коробки первый попавшийся кубик.
Возможно следующее из трех сочетаний: оба кубика синие, оба кубика белые, кубики различны по цвету.
Какова вероятность каждого из сочетаний?

Ответ к задачам №208 и №209 здесь: События и вероятности_2.

[1]     Гомбо́ Антуа́н (1607 – 29 декабря 1684) – французский писатель, известный также, как шевалье де Мере́, по имени персонажа его книг.

[2]    Паска́ль Блез (19 июня 1623 – 19 августа 1662) – французский математик, механик, физик, литератор, философ, теолог.

[3]    Пьер де Ферма́ (1607 – 12 января 1665) – французский математик-самоучка. Один из величайших математиков всех времён.

[4]    Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.

[5]    Христиа́н Гю́йгенс ван Зёйлихем (14 апреля 1629 – 8 июля 1695) – голландский механик, физик, математик, астроном, изобретатель.

[6]    Я́коб Берну́лли (6 января 1655 – 16 августа 1705) – швейцарский математик. Доказал частный случай закона больших чисел (теорема Бернулли).

[7]    Джеро́ламо Карда́но (24 сентября 1501 – 21 сентября 1576) – итальянский математик, инженер, философ, врач, астролог.