Задачи №210, 211, 212

Решим задачу №210:
У вас такое же количество кубиков и такие же условия вынимания кубиков, что и в задаче №209.
Необходимо найти вероятность вынуть:

• вынуть по крайней мере один синий кубик;
• вынуть хотя бы один белый кубик;
• вынуть первым синий кубик;
• вынуть белый кубик последним.

Напомню условия задачи №209:
В коробке лежат 3 синих и 4 белых кубика.
Вы вынимаете один кубик, затем кладете его обратно и перемешиваете содержимое. После этого вы снова вынимаете из коробки первый попавшийся кубик.

Для наглядности при решении задачи №209 мы составили таблицу (рис. 1)

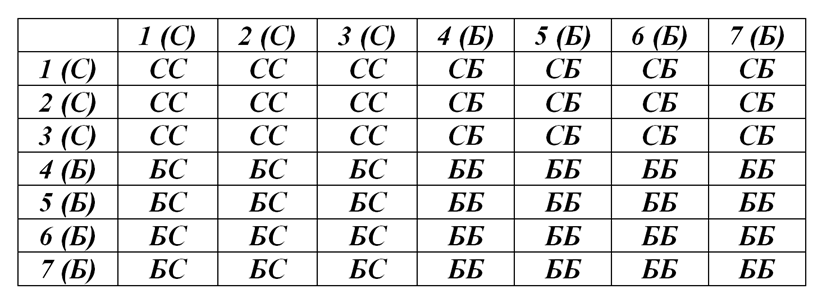
Теперь ответим на вопросы задачи №210, воспользовавшись вышеуказанной таблицей или, как мы делали при решении задачи №209, вычислив количество требуемых нам исходов.

Необходимо найти вероятность вынуть:

• вынуть по крайней мере один синий кубик;
• вынуть хотя бы один белый кубик;
• вынуть первым синий кубик;
• вынуть белый кубик последним.

Первый вопрос: вероятность вынуть по крайней мере один белый кубик.
Найдем количество возможных исходов:
СС – 9 возможных исходов;
БС – 12 возможных исходов;
СБ – 12 возможных исходов.
Всего у нас 49 равновозможных исхода вынимания кубиков.
Значит, вероятность вынуть по крайней мере один синий кубик равна:
(9+12+12)/49 = 33/49

Второй вопрос: вероятность вынуть по крайней мере один белый кубик.
Аналогично найдем количество возможных исходов, удовлетворяющих нашему требованию:
БС + СБ + ББ = 40
Вероятность вынуть по крайней мере один белый кубик равна:
40/49

Третий вопрос: вероятность вынуть первым синий кубик.
Обратите внимание на то, что данный вопрос сводит задачу к одному испытанию (первому выниманию кубиков из коробки). Это означает, что задача решается аналогично задаче №208. То есть, у нас всего 7 равновозможных исходов при вынимании кубика. Синих кубиков в нашей коробке всего 3.
Значит, вероятность того, что первым будет вынут синий кубик равна:
3/7

Четвертый вопрос: вероятность вынуть белый кубик последним.
И снова задача сводится к одному испытанию, но уже второму, так как результаты первого испытания не влияют на вероятность второго испытания.
Значит, вероятность вынуть белый кубик при втором испытании равна:
4/7

Обратите внимание на то, что при решении задач №209 и №210 мы, кроме использования таблицы, которая позволяет наглядно увидеть возможные варианты, могли воспользоваться и методами комбинаторики, вычислив возможные варианты (см.решение к задаче №209).

Решим задачу №211:
У вас две классических игральных кости с шестью гранями и числами на гранях от 1 до 6.
При подбрасывании любая из шести граней может оказаться верхней.
Вы подбрасываете обе игральные кости.
Необходимо найти вероятность того, что сумма очков (чисел) на верхних гранях:

• меньше 9;
• больше 7;
• делится на 3;
• четна.

При бросании двух костей имеется 36 равновозможных исходов – 36 пар возможных сочетаний чисел на верхних гранях костей.

Можно составить таблицу, в которой в левом столбце будут отражены возможные варианты числе на первой кости, а в верхней строке – возможные варианты чисел на второй кости. На пересечении отразим сумму числе на обеих костях (рисунок 2).

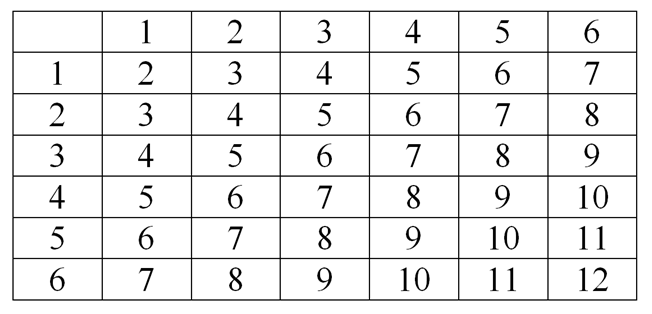
Подсчитав результаты, удовлетворяющие условиям, указанным в вопросах, мы можем найти, что:

• вероятность того, что сумма очков (чисел) на верхних гранях меньше 9, равна:

26/36 или 13/18

• вероятность того, что сумма очков (чисел) на верхних гранях больше 7, равна:

15/36 или 5/12

• вероятность того, что сумма очков (чисел) на верхних гранях делится на 3, равна:

12/36 или 1/3

• вероятность того, что сумма очков (чисел) на верхних гранях четна, равна:

18/36 или 1/2

Попытайтесь вычислить количество результатов, удовлетворяющим условиям, указанным в вопросах, без использования таблицы.

Решим задачу №212:
Вы играете с равным вам по силам противником игру. Например, в шахматы. Или, допустим, в теннис.
Что вероятнее: выиграть у равного вам по силам противника три партии из четырех или пять партий из восьми?

Прежде, чем перейти к решению задачи, необходимо условиться, что мы разбираем чисто теоретический вопрос, а потому оговорим некоторые условности:

• при равном большом количестве партий половина партий может закончиться победой первого игрока, а половина – победой второго игрока;
• результаты одних партий не влияют на результаты других партий (исключаем эмоциональную составляющую).

Допустим, игроки сыграли 4 партии. Для четырех партий возможно 16 последовательностей побед и поражений первого игрока:

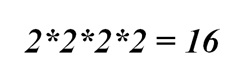
Рассмотрим случай, когда игроки сыграли n матчей из двух партий каждый. Первый игрок может выиграть в первой партии в n/2 матчах. Результат первой партии не влияет на результат второй партии. Значит, в половине вторых партий матчей, в которых первый игрок выиграл, он может проиграть:

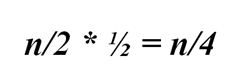
Если рассматривать другие события, например, победу второго игрока в обеих партиях, то такие события будут иметь место также в n/4 матчах.

Можно сформулировать, что вероятность события «исход первого опыта А, а второго – В» равняется произведению вероятности события «исход первого опыта есть А» и вероятности события «исход второго опыта есть В».

Событие, которое мы рассматриваем в задаче, – «победа в трех партиях». Мы рассматриваем не три победы подряд, а «победу в трех случаях из четырех». Этому событию благоприятны 4 исхода, так как единственное поражение может стоять на одном из четырех мест ряда партий.
Значит, вероятность выиграть 3 партии из 4 у равного по силе противника равна 4/16 или ¼.

Для состязаний из восьми партий количество равновозможных исходов побед и поражений первого игрока равно:
2⁸ = 256

Нам необходимо найти ответ на вопрос: сколько существует вариантов подмножества из пяти элементов (побед) в множестве из восьми элементов (сочетаний)?
И тут нам на помощь придет комбинаторика:
(8*7*6*5*4)/(5*4*3*2*1) = 8*7 = 56

Значит, вероятность выиграть пять партий из восьми у равного по силе противника равна

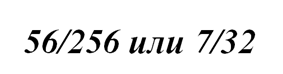
Вероятность выиграть три партии из четырех составила ¼ = 8/32.

То есть, вероятность выиграть у равного по силам противника три партии из четырех (1/4) больше, чем вероятность выиграть или пять партий из восьми (7/32).