События и вероятности_3. Задачи №213, 214, 215

В «События и вероятности» была описана задача (задача №207), предложенная французским писателем Антуаном Гомбо[1] на одном из частных математических вечеров. Помимо ранее описанной задачи, Гомбо (шевалье де Мере) предложил Паскалю[2] решить и такую задачу (задача №213):
Одновременно бросают три игральных кости (кубики с нанесенными на грани числами от 1 до 6).
Что вероятнее: что сумма очков на верхних гранях равна 11 или то, что эта сумма равна 12?
Каковы вероятности этих событий?

Решая эту задачу, сам шевалье де Мере (Гомбо) рассуждал следующим образом:
Необходимо найти, сколькими способами можно представить 11 и 12 в виде суммы трех натуральных слагаемых (у нас три игральные кости), каждое из которых не превосходит 6.
Выпишем суммы в порядке возрастания слагаемых, начиная с 11.
Если наименьшее слагаемое – 1, то

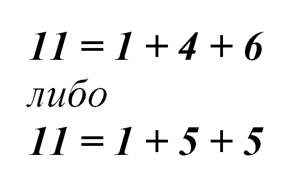
Если наименьшее слагаемое – 2, то

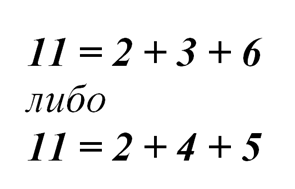
Если наименьшее слагаемое – 3, то

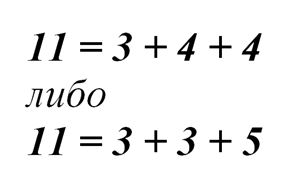
Этими шестью случаями исчерпываются все возможные варианты представить 11 в виде суммы из трех чисел, нанесенных на грани игральных костей.
Аналогично можно представить и число 12 шестью возможными способами:

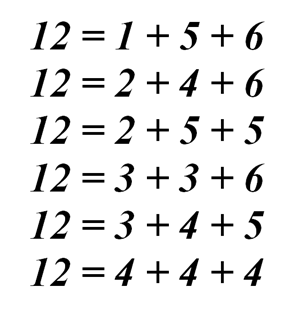
Отсюда, заключил Гомбо, сумма очков 11 может встретиться с той же частотой, что и сумма очков 12.

Проведя множество подбрасываний трех кубиков, Гомбо отметил, что сумма очков равная 11 встречалось чаще. То есть, теоретический расчет вероятности оказался неверен. За разъяснениями Гомбо обратился к Паскалю.
Блез Паскаль решил эту задачу иначе, опровергнув рассуждения Гомбо.

Попробуйте решить задачу Гомбо (задачу №213) и найти ошибку в его рассуждениях.

Предлагаю попытаться решить и следующие задачи:
Задача №214
Какова вероятность того, что наудачу выбранное четырехзначное число составлено только из нечетных цифр?

Задача №215
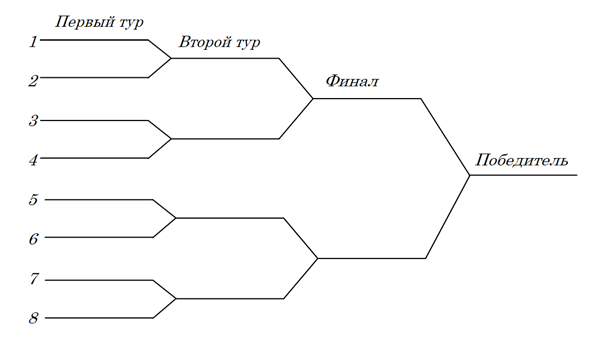
Представьте, что проводится турнир по олимпийской системе (плей-офф). Допустим, это греко-римская борьба. Всего восемь участников.
Номер участника определяет его положение в турнирной таблице (рис. 1), но не привязан к мастерству участника соревнований.
Предположим, что есть некий лучший по мастерству участник, который всегда побеждает остальных участников соревнований.
Есть также второй по мастерству участник, который, побеждая остальных участников соревнований, проигрывает только лучшему участнику.
Исходя из системы (см. рисунок 1), второе место займет тот участник, который проиграет в финале.
Какова вероятность того, что второе место займет второй по мастерству участник?

Ответы к задачам №213, 214, 215 здесь: События и вероятности_4.

[1]     Гомбо́ Антуа́н (1607 – 29 декабря 1684) – французский писатель, известный также, как шевалье де Мере́, по имени персонажа его книг.

[2]    Паска́ль Блез (19 июня 1623 – 19 августа 1662) – французский математик, механик, физик, литератор, философ, теолог.