Задачи №227, 228, 229

Решим две задачи из цикла «задачи на движение». В качестве примера такой задачи и решения к ней можете рассмотреть задачу №96. Пароходы.
Первоначально решим задачу Исаака Ньютона[1] (задача №227):
Два почтальона A и B, которых разделяет расстояние в 59 миль, выезжают утром навстречу друг другу: A делает за 2 часа 7 миль, а B – за 3 часа 8 миль. При этом B отправляется в путь часом позже A. Требуется найти, сколько миль проедет B до встречи с A?

Для решения этой задачи построим график движения каждого почтальона.
График движения первого почтальона (А) мы построим от пересечения осей Х (часы) и Y (мили) вверх.

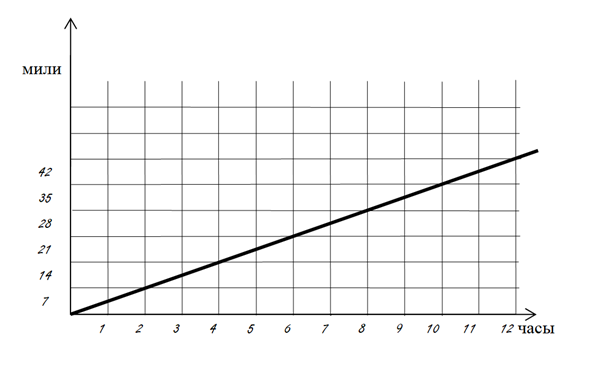
Так как второй почтальон (В) движется навстречу первому почтальону и начинает движение через час, то график его движения мы построим от пересечения осей Х (часы) и Y (мили) вниз от первого часа:

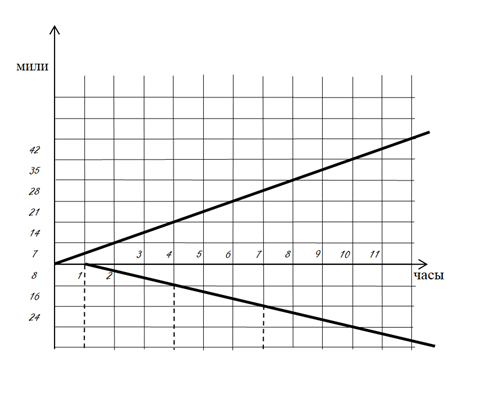
Точка пересечения графиков – 10 часов.
Через десять часов почтальон А проделает 35 миль, В проделает 24 мили.

Объединим оба графика:

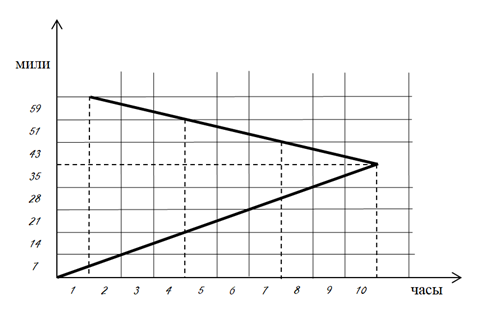
Можно решить эту задачу классическим способом.
Скорость первого почтальона 3½ миль/ч.
Скорость второго почтальона 2²̸₃ миль/ч.
В тот момент, когда В отправился в путь, А уже преодолел 3½ мили. Следовательно, расстояние между ними стало:

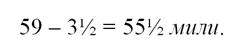
Скорость сближения:

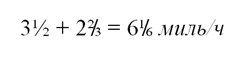
Почтальоны встретятся через

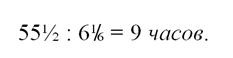
К моменту встречи А пройдет

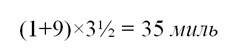
Почтальон В пройдет

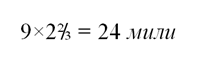
И еще одна задача, при решении которой поможет построение графика движения (задача №228):
Два джентльмена одновременно начали прогулку по аллее. Длина аллеи составляет 100 метров.
Мистер А за один час проходит 1 км. Мистер B за час проходит всего 600 метров.
Дойдя до конца аллеи, каждый поворачивается и идет обратно с прежней скоростью.
Встречаясь, джентльмены всякий раз делают приветственный поклон.
Вопрос:
Сколько раз джентльмены раскланиваются на протяжении первых 25 минут прогулки?
Сколько времени из этих 25 минут они шли в одном направлении?

Для решения этой задачи построим график движения каждого джентльмена

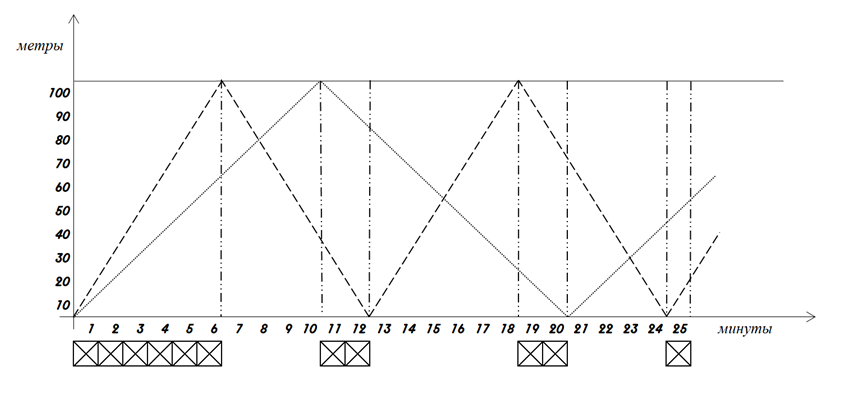
Легко подсчитать, что джентльмены встретились (раскланялись) за 25 минут три раза.
В одном направлении за 25 минут они прошли всего 11 минут.

Предлагаю вам решить другую задачу (задача №229):
В доме 123 жильца. Всем жильцам вместе 3813 лет.
Можно ли среди всех жильцов дома выбрать сотню, которым вместе будет не меньше 3 100 лет?
Для решения этой задачи целесообразно использовать принцип Дирихле.

Решение к задаче №229 здесь: И снова принцип Дирихле

[1] Исаак Ньютон (25 декабря 1642 года – 20 марта 1727 года по юлианскому календарю, действовавшему в Англии до 1752 года; или 4 января 1643 – 31 марта 1727 года по григорианскому календарю) – физик, математик, механик, астроном.