Задачи №233, 234

Решим задачу №233:
У вас есть 200 бананов, которые вы должны раздать 21 обезьянке.
Необходимо доказать, что при любом способе раздачи, найдется две обезьянки, которым достанется равное количество бананов. Возможность того, что кому-то бананов может не достаться вовсе, также рассматривается.

Решение этой задачи никак не связано с геометрией. Она дана просто для разминки и повторения самого принципа Дирихле.
Предположим, что мы применим такой «несправедливый» способ раздачи, при котором каждой последующей обезьянке мы даем на один банан больше, чем предыдущей:
Первой обезьянке не достанется бананов вовсе (мы ей потом вручим вкусное яблоко), второй дадим один банан, третьей – два банана, …, двадцать первой обезьянке дадим двадцать бананов.

При решении задачи №151 мы использовали формулу расчета суммы геометрической прогрессии. Геометрическая прогрессия – последовательность чисел, в которой первый член отличен от нуля, а каждый из последующих членов, начиная со второго, получается из предыдущего члена умножением его на ненулевое фиксированное для данной последовательности число (несколько упрощенное определение).
Для решения нашей задачи мы должны вычислить сумму для арифметической прогрессии (последовательность, в которой каждый следующий член можно найти, прибавив к предыдущему одно и то же число).

Сумму для арифметической прогрессии можно вычислить по формуле:

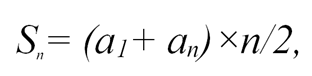
где

В нашем случае сумма будет равна 210. Но у нас всего 200 бананов. Это означает, что найдется две обезьянки, которым достанется равное количество бананов.

Решите задачу №234:
В квадрате со стороной 1 произвольно отмечаем 101 точку, причем никакие три точки не лежат на одной прямой.
Примечание: часть точек может располагаться и на сторонах квадрата.
Вопрос: Существует ли треугольник с вершинами в этих произвольных точках, площадь которого не больше 1/100?

Решение к задаче №234 здесь: Геометрия и принцип Дирихле_3