Задачи №238, 239

Решим задачу №238:
На квадратной шахматной доске размером n×n клеток расставлены ладьи (тура, башня). Условие, которому соответствует расстановка: если некоторое поле свободно, то общее количество ладей, стоящих на одной с этим полем горизонтали или на одной с ним вертикали, не менее n.
Необходимо доказать, что на доске имеется не менее чем следующее количество ладей:

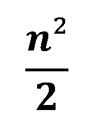
Предложенная задача несколько труднее, чем задачи №235, 236, 237. Тем не менее, если вы внимательно изучили решения вышеуказанных задач, то вполне сможете справиться и с этой.

Для решения задачи, как вы наверняка догадались, требуется рассмотреть ту из 2n линий (вертикалей и горизонталей) шахматной доски, на которой стоит меньше всего ладей.
Вполне может оказаться, что линий, одинаково заполненных ладьями, несколько. Тогда мы выберем любую из таковых линий.
Предположим, что выбранная нами линия – горизонталь. Вы можете выбрать вертикаль, но очевидно, что поворот шахматной доски на 90 градусов превращает любую горизонталь в вертикаль и наоборот.

Обозначим число фигур (ладей) на выбранной горизонтали буквой k.
Если

то на каждой из n линий не менее

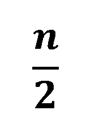
фигур, а на доске всего не менее

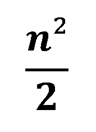
фигур.

Предположим, что

Тогда на рассматриваемой горизонтали

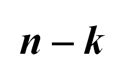
свободных полей.

Следовательно, и каждая вертикаль, проходящая через такое поле, содержит не менее

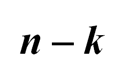
фигур (ладей). Все такие вертикали, очевидно, содержат не менее

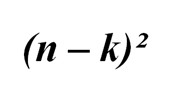
фигур. Остальные k вертикалей содержат не менее чем по k фигур каждая (см. условия выбора числа k).

Всего на нашей доске находится фигур, не менее чем

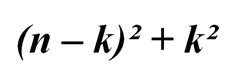
Для решения задачи нам необходимо доказать, что

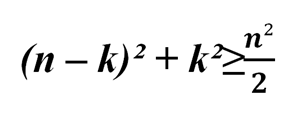
Один из способов доказать данное утверждение следующий.
Обозначим буквой x число

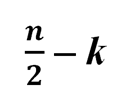
Тогда

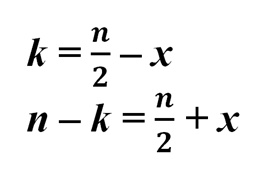
Отсюда

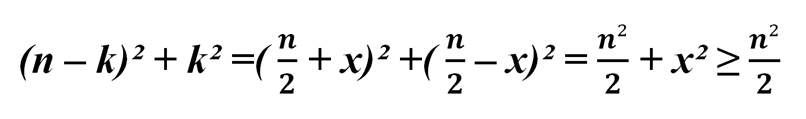
что и требовалось доказать.

Если n – четное число, то можно найти удовлетворяющую условиям задачи расстановку, содержащую количество ладей

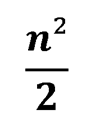
Для этого достаточно расставить наши шахматные фигуры на все белые или на все черные поля.
Если же n является нечетным числом, то расставить

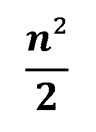
фигур нельзя, так как указанное число нецелое. Но можно расставить следующее количество фигур

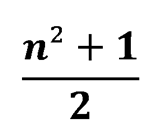
Как вы думаете, как это можно сделать?

Решите задачу №239:
Пусть n² неотрицательных чисел расположены в виде квадратной таблицы, содержащей n строк и n столбцов. При размещении должно быть выполнено следующее условие: если на некотором месте таблицы записан нуль, то сумма чисел столбца и строки, содержащих такую запись, не менее следующего значения:

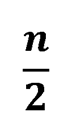
Докажите, что сумма всех чисел таблицы не менее чем

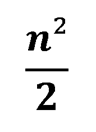
Решение задачи №239 можно посмотреть здесь: Правило (принцип) «крайнего»_4.