Задачи №239, 240

Решим задачу №239:
Пусть n² неотрицательных чисел расположены в виде квадратной таблицы, содержащей n строк и n столбцов. При размещении должно быть выполнено следующее условие: если на некотором месте таблицы записан нуль, то сумма чисел столбца и строки, содержащих такую запись, не менее следующего значения:

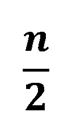
Докажите, что сумма всех чисел таблицы не менее чем

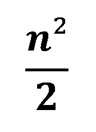
Решение этой задачи почти ничем не отличается от решения задачи №238.
Если n – число четное (см. задачу №238), то условиям задачи удовлетворяет таблица, на одной из диагоналей которой стоят числа, равные

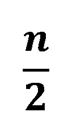
а на остальных – нули.
Сумма чисел этой таблицы будет равна

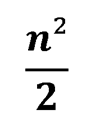
Решите еще одну задачу, используя правило «крайнего» (задача №240):
На плоскости заданы n точек. Никакие три из заданных точек не лежат на одной прямой.
Необходимо доказать, что существует окружность, проходящая через три из данных точек, но не содержащая внутри ни одной из данных точек.

Решение задачи №240 можно посмотреть здесь: Правило (принцип) «крайнего»_5