Часть 1. Зарождение алгебры

Алгебра, как искусство решения уравнений, зародилось у вавилонян[1], которые решали уравнения второй степени и некоторые виды уравнений третьей степени. При решении уравнений третьей степени ими использовались специальные таблицы. Записи вавилоняне делали на глиняных табличках. Часть глиняных табличек Вавилонского царства, сохранившихся до настоящего времени, представляет собой своеобразную математическую энциклопедию – свод достижений вавилонян к периоду около двухтысячного года до н.э. Из этой энциклопедии видно, что уже к эпохе Хамураппи[2] вавилоняне имели достаточно удобные способы вычисления для решения практических задач, связанных с земледелием, орошением, торговлей, решали линейные и квадратные уравнения,

В отличие от вавилонян, делавших записи на глиняных табличках, египтяне использовали папирус, более удобный, но менее долговечный. Известны также египетские деревянные таблички, записи на коже (кожаные свитки). Большая часть сохранившихся памятников (записей) относится к периоду Среднего царства[3]. В основном это копии, переписанные в более поздние периоды.

К памятникам древнеегипетских текстов, посвященных математике, относятся, например:

• Математические папирусы Лахуна, также известные как Математические папирусы Кахуна. Папирусы Лахуна представляют собой собрание текстов, включающее административные тексты, медицинские тексты, ветеринарные тексты и фрагменты, посвященные математике.
• Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда). Это древнеегипетское учебное руководство по арифметике и геометрии периода XII династии Среднего царства (1985— 1795 гг. до н. э.).
• Папирусы Рейснера, которые датируются периодом правления Сенсусерта I, фараона Древнего Египта, правившего в XIX веке до н.э.

Древние египтяне уже составляли уравнения с неизвестными. В качестве примера можно привести задачу из математического папируса Ахмеса: «Найти число, если известно, что от прибавления к нему ⅔ его и вычитания из результата его трети получается 10». Или, например, можете ознакомиться с рисунком 1 (основная статья «Письменная нумерация»), содержащим задачу, написанную иероглифами, и пояснение к нему.

Рисунок 1
Читается уравнение справа налево: «Куча (неизвестное), ⅔, ½, ⅐, целое (кучи) составляет 33». В переложении на современный способ записи: х+⅔х+½х+⅐х=33.

Египтяне при решении задач, которые в настоящее время решаются с применением уравнений первой степени, пользовались методом «ложного положения»[4]. В старых русских руководствах по решению задач «правило ложного положения» носило название «фальшивое правило».

Следует отметить, что самостоятельным путем в развитии алгебры шли индусы. Среди наиболее древних из сохранившихся индийских текстов, содержащих математические сведения, выделяется серия книг «Шульба-сутры»^[5], самые ранние редакции которых относятся к VI веку до н.э. Математическая мысль древней Индии оказала влияние на развитие математики древней Греции.

Первые дошедшие до нас индийские «сиддханты» (научные сочинения) относятся уже к IV – V векам н.э. И в них уже заметно влияние математиков древней Греции.

В V – IV веках в трудах индийского астронома и математика Ариабхаты[6] встречаются намеки на общее решение уравнений первой степени вида ах+by=с (диофантовых уравнений). Известный индийский математик и астроном Брахмагупта[7] (VII век) также излагал решение для данного вида уравнений.

Другой индийский математик и астроном Бха́скара (Бхаскара I)[8] написал два астрономических трактата «Махабхаскария» и «Лагхубхаскакия», в которых, в частности, рассматривал элементы тригонометрии и неопределённые линейные уравнения.

Общий метод для решения в целых числах неопределенных уравнений первой степени с целыми коэффициентами в Индии был назван методом рассеивания (размельчения).

Многие из трудов индийских ученых были переведены на арабский язык и частично дошли до Европы.

Первые китайские учебники математики относятся к XI веку до н.э. – началу правления династии Чжоу^[9]. Китайские ученые были вполне осведомлены о достижениях древнегреческих и индийских ученых, успешно решали уравнения первой степени и их системы, квадратные уравнения. Математико-астрономический «Трактат об измерительном шесте» и энциклопедический трактат «Математика в девяти книгах»^[10] (окончательную редакцию которой сделал Чжан Цан^[11] во II в. до н.э.), опубликованы в Китае во II веке до н.э. Это наиболее ранние дошедшие до нас сочинения по математике китайских ученых. С одной из задач, изложенных в трактате, вы можете ознакомиться здесь. Считается, что «Математика в девяти книгах» представляет собой компиляцию более ранних трудов разных китайских авторов, написанных в X век до н.э. – II веке до н.э. Упоминаемое в китайских летописях, но не дошедшее до нас сочинение «Цзю шу», относимое к XII век до н.э., оглавление которого во многом совпадает с оглавлением «Математики в девяти книгах», позволяет говорить о том, что китайская математическая мысль имеет очень древние корни.

В III веке н.э. выходит «Математический трактат» («Сунь Цзы Суань Цзин» или «Счетный канон Сунь-цзы») Сунь-цзы[12].

В I – V вв. н.э. китайцы производят последовательное уточнение числа «пи». Уже к V веку китайцы разрабатывают метод «фан-чэн» для решения систем произвольного числа линейных уравнений, способом «тянь-юань» численно решают уравнения любой степени.

Греческие геометры владели основными алгебраическими операциями, но ограничивали их применение к отрезкам прямой. Греки, судя по всему, были знакомы с работами в области математики Египта, Вавилона, Индии. Так, в жизнеописаниях Пифагора[13] рассказывается о посещении им Индии, Вавилона, Египта, что, несомненно, сыграло свою роль в его работах. Но наибольшее значение именно для алгебры имеет фигура греческого математика Диофанта[14], который жил и работал в более поздний период.

Точные годы жизни Диофанта неизвестны. Предполагают, что он жил в III век до н.э. В одном из древних рукописных сборников задач жизнь Диофанта описывается в виде алгебраической задачи, представляющей надгробную надпись на его могиле:

Прах Диофанта гробница покоит; дивись ей — и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.[15]

Задача-загадка сводится к составлению и решению уравнения:

⅙х + ⅟₁₂х + ⅐х + 5 + ⅟₂х + 4 = х,

при решении которого мы находим, что х = 84, т.е. количество лет, прожитых Диофантом[16].

Будучи автором «Арифметики», Диофа́нт нередко упоминается как «отец алгебры».

В сохранившихся книгах Диофанта содержится 189 задач с решениям. В его книгах нет систематической теории, методы решений меняются от случая к случаю, но используемые им методы решений неопределенных уравнений составляют основной вклад в развитие математики. Диофант использует числовое решение уравнений первой и второй степени, применяя только один знак для неизвестного. В качестве нескольких неизвестных он применял произвольные числа, вместо которых можно взять любые другие. Пример таких решений вы можете посмотреть в ответах к задаче №51 («из «Арифметики» Диофанта»). На рисунке 2 представлено Диофантово решение системы уравнений
х+у=20
х²–у²=80

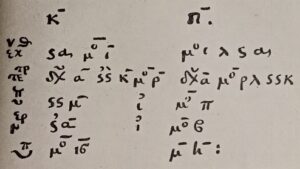
Рисунок 2

Аль-Хорезми[17] в начале IX века издает книгу «Китаб-аль-джебр аль-мукабала»[18] («Краткая книга о восполнении и противопоставлении»). «Восстановление» в книге означает превращение вычитаемого (в привычном нам обозначении – отрицательного) числа в положительное при перенесении из одной половины уравнения в другую. Во времена Аль-Хорезми отрицательные числа не считались настоящими числами, а потому операция «аль-джебр» (алгебра), при которой число как бы возвращалось из небытия в бытие, казалась чудом.

Интересно, что термин «алгебра» использовался арабами и в медицине – восстановление здоровья врачевателем также называлось алгеброй. Такое использование термина «алгебра» в смысле «восстановление» можно наблюдать не только у арабов. В главе XV второй части романа испанского писателя Мигеля де Сервантеса[19] «Дон Кихот»[20] описывается, как один из героев, получив травмы и нуждаясь в лечении, прибегает к услугам «алгебраиста». Вот этот отрывок на испанском языке: «En esto fueron razonando los dos, hasta que llegaron a un pueblo donde fue ventura hallar un algebrista, con quien se curó el Sansón desgraciado».

В переводе на русский язык это звучит так: «Об этом они рассуждали вдвоем, пока не прибыли в деревушку, где им посчастливилось найти алгебраиста, с помощью которого вылечился несчастный Самсон».

В первоначальных переводах романа использовалось именно слово «алгебраист». В более поздних версиях «алгебраист» был заменен на «костоправ», а затем на «цирюльник»[21].

Наличие в испанском (и не только) языке слова «алгебраист» в значении «врачеватель» объясняется тем, что арабы, в течение нескольких столетий владевшие Пиренейским полуостровом[22], привнесли туда многое из своей культуры, а также многое из того, что было заимствовано ими из культур других народов, в частности народов Средней Азии[23]. Арабы принесли в покоренные ими страны сочинения по математике аль-Хорезми, аль-Фергани[24] и других ученых, переводы греческих авторов. Именно поэтому многие арабские слова прочно вошли в испанский и португальский языки, в том числе и слова «алгебра», «алгебраист» в тех значениях, в которых эти слова использовались у арабов.

Книга Аль-Хорезми «Китаб-аль-джебр аль-мукабала» в XII веке была переведена на латинский язык^[25] и послужила родоначальницей европейских учебников алгебры. Переводы математических трактатов Аль-Хорезми использовались в европейских университетах как основные учебники по математике вплоть до XVI века.

Среди крупнейших алгебраистов (ученых – математиков) необходимо отметить ученого и поэта Омара Хайама^[26]. Родившийся в семье ремесленника, он собственными стараниями получил квалификацию хаки́ма, то есть врача. Омар Хайам изучал трактаты Сабита ибн Курра аль-Харрани́^[27], древнегреческих математиков. Самаркандский друг Омара Хайама Мир Абу Тахир Ходжи Самарканди, оказал ему материальную помощь, дал возможность продолжать научные исследования. Именно ему и посвящен трактат «О доказательствах задач алгебры и алмукабалы» (алгебра), написанный Омаром Хайамом в 1069-1074 годы.

Трактат «О доказательствах задач алгебры и алмукабалы» содержал почти всю совокупность алгебраических знаний того времени. В нем излагались решения уравнений первой, второй и третьей степени. Именно в этом трактате Омар Хайам пишет, что алгебра – это наука об определении неизвестных величин, состоящих в некоторых отношениях с величинами известными. Это первое определение алгебры, как науки, дошедшее до нас. В трактате Омар Хайам описывает решение геометрическими методами уравнений третьей степени. Алгебраические методы решения этих уравнений были найдены в Европе только в середине XVI века.

Узбекский и персидский математик Гияс-ад-дин Джамшид ибн Масуд аль-Каши^[28] в начале XV века в своей книге «Поучения об окружности» впервые вводит в науку десятичные дроби, на 175 лет опередив появление десятичных дробей в Европе.

[1]    Вавилонское царство (Вавило́ния) – древний регион и царство между Тигром и Ефратом на юге Месопотамии (территория современного Ирака), возникшее в начале II тысячелетия до н.э.

[2]    Хаммура́пи – Вавилонский царь. Правил приблизительно в 1793-1750 годах годах до н.э.

[3]    Среднее царство – эпоха истории Древнего Египта между 2040 и 1783 (или 1640) до н.э.

[4]    Правило ложного положения — ранее распространенный метод решения уравнений, основанный на замене неизвестного произвольным числом и последующим его нахождением на основе пропорциональности.

[5]    Шу́льба-су́тры – сутры (своды высказываний), относящиеся к ритуалу шраута (ритуалистическая традиция) и содержащие геометрические данные по сооружению алтаря для жертвенного огня.

[6]    Ариабха́та (Ариабха́тта, Арьябха́та) (476 – 550) – индийский математик и астроном.

[7]    Брахмагупта (Брамагупта) (около 598 – 670) – индийский математик и астроном.

[8]    Бха́скара (около 600 – около 680) – индийский математик и астроном. В различных источниках встречается наименование Бхаскара I, чтобы отличить его от другого индийского учёного, Бха́скара (Бхаскара II), жившего в XII веке.

[9]    Эпоха Чжоу (с 1045 до н.э. по 221 до н.э.) – эпоха в истории Китая, время правления рода Цзи.

[10] «Математика в девяти книгах» – энциклопедия знаний древнекитайских математиков. Компиляция трудов разных китайских авторов, написанных в X век до н.э. – II веке до н.э.

[11] Чжан Цан (253–152 до н.э.) – ученый-конфуцианец.

[12] Сунь Цзы (время жизни известно лишь приблизительно: III – V века н.э.) – китайский математик и астроном.

[13] Пифаго́р Са́мосский (около 570 – 490 годов до н.э.) – древнегреческий философ, математик, теоретик музыки.

[14] Диофа́нт Александри́йский (предположительно III век н.э.) – древнегреческий математик. Автор «Арифметики».

[15] Перевод Ивана Николаевича Весело́вского.

[16] Достоверность данного утверждения не подтверждена.

[17] Абу́ Абдулла́х (или Абу Джафар) Муха́ммад ибн Муса́ аль-Хорезми́ – (около 783 – около 850) – среднеазиатский ученый, математик, астроном, географ, историк.

[18] «Краткая книга о восполнении и противопоставлении» – математический трактат Муха́ммада ибн Мусы аль-Хорезми́, от названия которого произошёл термин «алгебра».

[19] Миге́ль де Серва́нтес Сааве́дра (предположительно 29 сентября 1547 – 22 апреля 1616) – испанский писатель.

[20] «Хитроу́мный ида́льго Дон Кихо́т Лама́нчский» – роман испанского писателя Миге́ля де Серва́нтеса о приключениях одноименного героя. Был опубликован в двух томах. Первый вышел в 1605 году, второй – в 1615 году.

[21] Цирю́льник – исторически парикмахер и банщик, владеющий элементарными приёмами хирургии.

[22] Пирене́йский (Иберийский) полуо́стров – полуостров на юго-западе Европы.

[23] Сре́дняя А́зия – историко-географический регион в Евразии.

[24] Абу́-ль-Абба́с А́хмад ибн Муха́ммад аль-Ферга́ни (798 – 861) – один из крупнейших средневековых ученых IX века, астроном, математик и географ.

[25] Лати́нский язы́к (lingua Latina), или латы́нь – язык, употреблявшийся в Римской империи.

[26] Гия́с-ад-Ди́н Абу-ль-Фатх Ома́р ибн Ибрахи́м Хайя́м Нишапури́ (Ома́р Хайя́м) (18 мая 1048 – 4 декабря 1131) – персидский и таджикский философ, математик, астроном, поэт.

[27] Абуль-Хасан Сабит ибн Курра аль-Харрани́ (836 – 18 февраля 901) – астроном, математик, механик, врач.

[28] Гияс-ад-дин Джамшид ибн Масуд аль-Каши (1380 – 22 июня 1429) – узбекский и персидский ученый, математик, астроном.