Знаки неравенства («>», «<») появились в 1631 году (см. «Знаки равенства и неравенства»), но само понятие неравенства, как и понятие равенства, возникло еще в глубокой древности. До употребления знаков равенства и неравенства писали «равно», «больше», «меньше».
Вы можете попытаться доказать неравенства, описанные в V книге «Начал» Евклида[1] (смотри: задача №44). Указанная книга содержит теорию отношений и пропорций, разработанную Евдоксом Книдским[2]. Или изучите неравенства, изложенные в III веке в труде Паппа Александрийского[3] «Математическое собрание» (смотри: задача №45).
При развитии математической мысли без сравнения величин, без самих понятий «больше» и «меньше» нельзя было дойти до понятия «равенство», «тождество», «уравнение». С понятием неравенства связаны и приближенные вычисления, в том числе, вычисление π[4], метод исчерпывания, современное понятие предела и др.
Помимо знаков неравенства в теории и практических задачах встречаются знаки неравенства, соединенные со знаком равенства:
≥ – больше или равно (не меньше);
≤ – меньше или равно (не больше).
В отличие от неравенств, содержащих знак > или <, называемых строгими, такие неравенства (≥, ≤) называются нестрогими.

Символы и были введены в 1734 году французским математиком Пьером Буге[5]. Позже их стали записывать так: и
Сейчас, как уже указано выше, они обозначаются так: ≥ и ≤.
Но еще задолго до появления самих символов, уже описывались нестрогие неравенства. Например, в той же V книге «Начал» Евклида содержится неравенство:

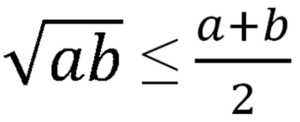
где  a, b ≥ 0. Словами оно выражается так: среднее геометрическое двух неотрицательных чисел не больше среднего арифметического этих чисел.
Можете проверить указанное неравенство на примерах.
Доказательство данного неравенства основывается на фундаментальном неравенстве, которое выражает неотрицательность квадрата любого[6] числа:
(l – m)^²≥ 0.
Здесь (l – m)^²= 0 только при условии l = m.
Из неравенства (l – m)^²≥ 0 вытекает:
l^² + m^² ≥ 2lm, или
(l^² + m^²)/2≥ lm

Положив l^² = а, m^² = b, получим неравенство

Французский математик Огюстен Луи Коши[7], обобщив неравенство  на 3, 4, 5, …, n неотрицательных чисел, доказал в 1821 году неравенство:

то есть среднее геометрическое n неотрицательных чисел не больше среднего арифметического этих чисел. Следует отметить, что равенство существует при условии, если только все n чисел равны между собой.

Вы можете проверить неравенство на примерах для n = 3, 5, 6.

Классическое доказательство неравенства  , данное Коши, основано на методе математической индукции[8]. В настоящее время известно множество различных доказательств указанного неравенства.

[1]    Евкли́д (примерно в период 325 – 265 годы до н.э.) – древнегреческий математик, геометр.

[2]    Евдо́кс Кни́дский (ок. 408 года до н.э. – ок. 355 года до н.э.) – древнегреческий математик, механик, астроном.

[3]    Папп Александри́йский (жил, по всей вероятности, в конце III или в начале IV века) – математик и механик эпохи позднего эллинизма.

[4]    π («пи») – математическая постоянная, равная отношению длины окружности к её диаметру.

[5]    Буге́ Пьер (16 февраля 1698 – 15 августа 1758) – французский физик, математик, астроном. Основатель фотометрии.

[6]    Подразумеваются действительные числа.

[7]    Огюсте́н Луи́ Коши́ (21 августа 1789 – 23 мая 1857) – французский математик, механик.

[8]    Математическая индукция – метод математического доказательства.