Ящик с носками

Ответ к задаче №1 Ящик с носками

Как мы уже разбирали в «События и вероятности», основную формулу классической теории вероятностей можно изложить так:

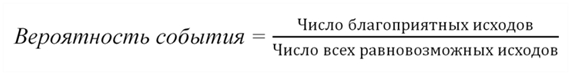
Эта формула подходит для случаев, когда исходы опыта равновозможны и надо только вычислить вероятность «благоприятного» исхода.

В нашем случае нет указания на конкретное количество носков в ящике шкафа. «Благоприятным» же считается вариант с двумя носками одинакового цвета – красного.
Обозначим количество красных носков через x, а количество черных носков через y.
Вероятность того, что первым мы вытянем именно красный носок, равна (см. формулу выше)

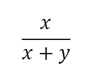
Если произойдет данное событие (мы вытянули первым красный носок), то вероятность вытянуть второй носок красного цвета при следующей попытке будет

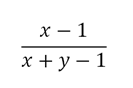
В условиях задачи указано, что вероятность вынуть один за другим два красных носка равна ½, или

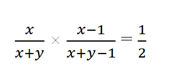
Можно начать перебирать различные варианты значения y, начиная с единицы. Собственно, мы довольно быстро найдем ответ.
Пойдем другим путем и используем теоретический расчет.
Очевидно, что при наличии в ящике черных носков (y > 0)

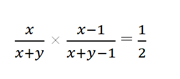
Обе части нашего неравенства неотрицательны. Следовательно, мы можем возвести эти части в квадрат, получив неравенство того же смысла.
Вероятность вынуть один за другим два красных носка (см. выше) равна ½, или

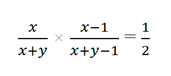
Учитывая изложенное выше, мы можем получить неравенство

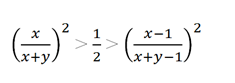
Извлечем квадратные корни (для x > 1) и получим

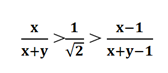
Для первого неравенства

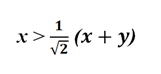
или, если умножить каждую часть на

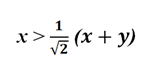
мы получим

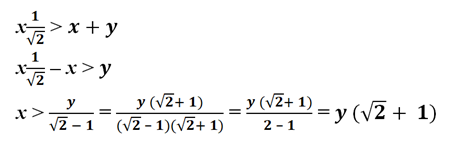
Из второго неравенства, выполнив необходимые преобразования, находим

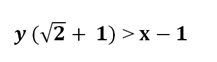
Получаем

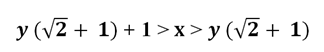
Если y = 1, то

3,414 > x > 2,414

Будем считать, что носки в ящике целые.

Значит, y = 1, x =3.

Проверим вероятность

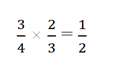
Это соответствует условиям задачи. Таким образом, минимальное количество носков в ящике: 4.

Если рассматривать четное количество черных носков, то перебирая значения от 2 (пары), мы придем к тому, что при шести черных носках (трех парах) x (красные носки) будет находиться в диапазоне от 14,5 до 15,5. Подходящее x будет равно 15.

Проверим вероятность

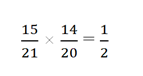
Это соответствует условиям задачи. Таким образом, минимально возможное число носков в ящике, если число черных носков четно: 21.

Ответ к нашей задаче:

а) 4

б) 21

Конечно же, это не единственные возможные варианты для вероятности достать два красных носка, а только варианты с минимальным значением (см. условия задачи). Для поиска всех возможных вариантов необходимо воспользоваться методами теории чисел.

Задача №1 здесь