Часть 2. История алгебры в XVI веке

Часть 1. Зарождение алгебры

Рисунок 1. Математики XVI века

В Европе в XVI веке было положено начало перехода к новому этапу развития алгебры, как науки: создана алгебраическая символика (см. «О буквенных коэффициентах»), найдены алгебраические решения уравнений третьей и четвертой степени.
Прогресс? Да, если не учитывать некоторые особенности. А именно то, что развитие алгебры сдерживалось, как это ни парадоксально, теми, кто её развивал. Вызвано это было традицией проведения своеобразных математических поединков-диспутов, во время которых противники предлагали друг другу задачи для решения их на месте или в определенный срок. Такие «поединки» проводились на многолюдных собраниях. Побеждал тот из противников, кто решал большее количество задач. И если победитель получал славу, денежный приз и возможность занять университетскую кафедру или иную почетную должность, то потерпевший, как часто случалось, терял занимаемое им место. Таким образом, утаивание открытий, умение держать их в строгом секрете имело особое значение для карьеры их авторов. Алгебра, называемая «Великим искусством»[1], занимала первое место в проводимых поединках-диспутах XVI века. Город Болонья[2], славившийся своим университетом[3], был излюбленным местом проведения таких «поединков». Именно в Болонском университете работали многие ученые с мировым именем: Лука Пачоли[4], Николай Коперник[5] и др.
Участники алгебраических диспутов находились в том положении, когда вновь открытые формулы решения того или иного типа уравнений, алгоритм, с помощью которого можно было решить значительное количество задач, необходимо было скрывать для того, чтобы остаться при должности, приносящей доход. Научные диспуты, которые, казалось бы, были направлены на выявление самых одаренных, приводили к сокрытию научных достижений. Ученый, победивший в диспуте, не был заинтересован передать знания своим ученикам, дабы не быть снизвергнутым с занимаемой должности.
В начале XVI века профессор Болонского университета Сципион дель-Ферро[6] находит алгебраическое решение уравнений третьей степени вида

х³ + px = q, (1)

где p, q – положительные числа. И это решение, по описанным выше причинам долгое время держится в строжайшем секрете. Только два ученика профессора знали об открытом им способе решения.

После смерти Сципиона дель-Ферро его ученик Антонио Марио Фиоре[7] вызвал на публичный диспут одного из виднейших математиков того времени – Никколо Тарталья[8].

Рисунок 2. Никколо Тарталья

Стоит немного подробнее описать этого замечательного математика – Никколо Тарталья. Его настоящая фамилия – Фонтана. Он родился в городе Брешиа[9] в 1499 году (по другим данным – в 1500 или 1501 году). Его отец умер, когда Никколо было всего шесть лет, оставив семью в полной нищете. В 1512 году город был оккупирован французскими войсками[10]. Зверства, чинимые французскими солдатами, коснулись и юного Никколо – он получил удар саблей, вследствие чего у него был рассечен подбородок и язык. Мать выходила Никколо, но говорить свободно он уже никогда не мог. Речь его была крайне невнятной, за что он и получил от товарищей прозвище «заика» (tartaglia)[11]. Прозвище это сделалось его фамилией.
Никколо, не смотря на тяжелые материальные условия, упорно изучал математику. Нередко свои вычисления он делал на досках и камнях (вспомните Архимеда[12] с его записями на песке, над которыми он, по преданию, и погиб).
В 1535 году, ко времени вызова на поединок со стороны Фиоре, Тарталья уже славился как первоклассный ученый и занимал кафедру математики в Вероне[13].
Алгебраическое решение кубических уравнений, то есть нахождение общей формулы, выражающей корни любого уравнения третьей степени в зависимости от коэффициентов при помощи конечного числа алгебраических операций (сложения, вычитания, умножения, деления, возведения в степень, извлечения корней), являлось одной из самых актуальных проблем того времени. Если для уравнений второй степени такая формула была давно известна, то для уравнений третьей степени формулы ученые найти не могли.
Тарталья, получив вызов на математический поединок, понимает, что Фиоре обладает формулой для решения уравнений вида (1). Поэтому Тарталья, готовясь к диспуту, все свое время тратит на писки алгебраического решения кубических уравнений. Позже он напишет: «Я приложил всё свое рвение, усердие, умение, чтобы найти правило для решения кубических уравнений, и, благодаря благосклонной судьбе, мне удалось это сделать за восемь дней до срока».
На состоявшемся 20 февраля 1535 года диспуте Тарталья в течение двух часов решил 30 задач, предложенных ему Фиоре. При этом сам Фиоре не смог решить ни одной из тридцати задач, которые для него выбрал Тарталья. Фиоре признал себя побежденным, а Тарталья обрел знаменитость во всей Италии. Тем не менее, Тарталья предпочел держать найденную им формулу в секрете, намереваясь в последующем опубликовать её в своем труде по алгебре.
В 1539 году к Тарталье обращается Джераломо Кардано[14] с просьбой сообщить ему алгоритм решения кубических уравнений. Кардано дает «священную клятву» не раскрывать секрет. Тарталья соглашается предоставить Кардано формулу, но сообщает её не полностью, а лишь частично, тщательно маскируя полное решение.

Рисунок 3. Дж.Кардано

В 1542 году Кардано знакомится в Болонье с рукописями покойного дель-Ферро и открывает для себя недостающие части решения. Он публикует алгебраическое решение уравнения третьей степени в своем труде «Artis Magnae, Sive de Regulis Algebraicis» («Великое искусство, или Правила алгебры»). В этой же книге он приводит алгебраическое решение уравнения четвертой степени – открытие, сделанное одним из его учеников, Луиджи Феррари[15].

Тарталья обвиняет Кардано в нарушении данной им клятвы. Он пишет: «У меня вероломно похитили лучшее украшение моего труда по алгебре». Следует полемика между математиками и их сторонниками. Кардано оправдывает себя тем, что в книгу включены многие вещи, которые он нашел сам, а также решения, найденные его учеником – Луиджи Феррари.
В любом случае формула алгебраического решения уравнений третьей степени получила название «формула Кардано».
Тарталья публикует еще несколько трудов, в том числе «Общие исследования чисел и мер»[16], в котором впервые применяются круглые скобки, а также содержится таблица «биномиальных коэффициентов», получаемых при возведении в 1, 2, 3, …, n степень двучлена (бинома) «а + b».

Эти коэффициенты было принято располагать в виде «арифметического треугольника» – треугольной числовой таблицы (рисунок 4).

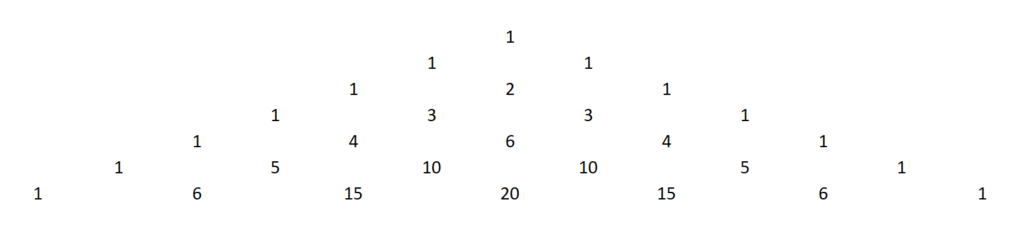
Рисунок 4. Треугольная числовая таблица

Интересно, что «арифметический треугольник» в разных странах носит разное название. Это связано с историей его появления в письменных источниках различных народов.
Наиболее древними являются упоминания о подобном «треугольнике» в трактате Чандамшастра («Чандас-шастра» или «Чандас-сутра», трактат о стихосложении) древнеиндийского математика Ачарья Пингала[17] (ок. II века до н.э.). Пингала в своей работе представляет первое известное науке описание двоичной системы счисления. Его описание двоичной системы счисления связано с перечислением ведийских размеров стихосложения с короткими и длинными слогами. Индийский математик Халаюдха[18] в X веке, в комментариях к Чандамшастра Пингалы уже подробнее описывает «арифметический треугольник», называемый им «меру-прастаара».
Омар Хайам[19] (см. также «Часть 1. Зарождение алгебры») в своих трудах (около 1100 года) исследует подобный «арифметический треугольник», поэтому в Иране «арифметический треугольник» носит имя «треугольником Хайяма».
Китайский математик Чжу Шицзе[20] в трактате «Яшмовое зеркало четырёх элементов» (1303 год) приводит изображение «треугольника» до n=8. При этом считается, что изображенный «треугольник» изобрёл другой китайский математик – Ян Хуэй[21], поэтому китайцы называют его треугольником Ян Хуэя (рисунок 5).

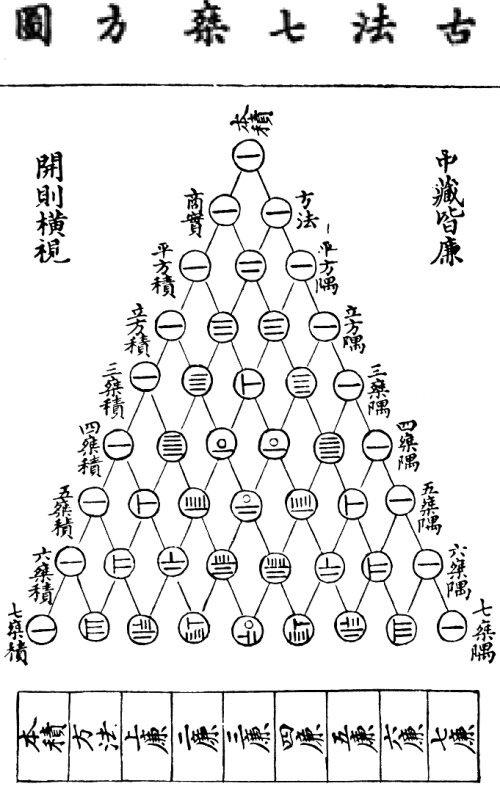
Рисунок 5. Треугольник Ян Хуэя

Персидский математик аль-Каши[22] описывает «треугольник» до n=9.
В Европе описание «треугольника» фигурирует у Петера Апина[23] (1527 год) и Михаэля Штифеля[24] (1544 год).

Рисунок 6. Петер Апиан

На титульном листе учебника арифметики, написанного в 1529 году Петером Апианом, изображён «арифметический треугольник» (рисунок 7).

Рисунок 7. Титульный лист «Арифметики» Петера Апиана

Для примера приведем изображение японского «арифметического треугольника», взятое из книги 1781 года (рисунок 78).

Рисунок 8. Японский «арифметический треугольник»

Наибольшую известность «треугольная таблица» получила в связи с работами Блеза Паскаля[25], почему часто называется «треугольником Паскаля».
В Италии «треугольником Паскаля» иногда называют «треугольником Тартальи», который описал подобную таблицу за сто лет до Паскаля, хотя приводимая Никколо Тартальей таблица и имела несколько иной вид.
Приведем некоторые свойства арифметического треугольника, которые описывает Тарталья в своей книге: по боковым сторонам треугольника стоят единицы; числа, симметричные относительно «высоты», то есть вертикального столбца треугольника (1, 2, 6, …) равны между собой; каждое число внутри треугольника образуется сложением двух стоящих над ним (справа и слева) чисел.
Указанная Тарталья схема позволяет построить аналогичные треугольники. Например, умножая строки арифметического треугольника на последовательные степени числа 2 (2¹, 2², 2³, …) получаем «треугольник»

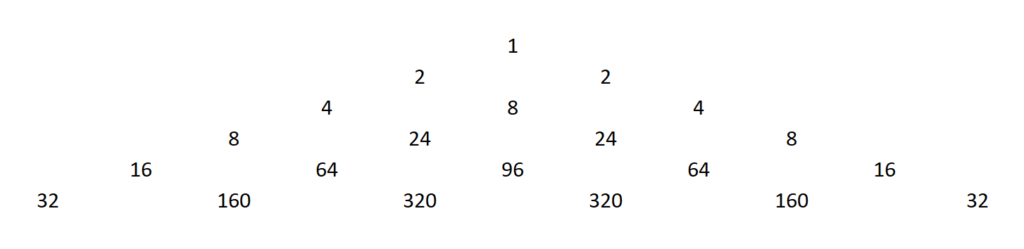
Рисунок 9. «Треугольник» Н. Тарталья

В указанном треугольнике первое и последнее числа каждой строки равны не единице, а последовательно степеням 2, т.е. 2, 4, 5, … Каждое число внутри треугольника равно произведению числа 2 на сумму двух чисел, стоящих над ним слева и справа. Например, 96=2*(24+24) или 64=2*(24+8) и т.п.

Книга Блеза Паскаля «Трактат об арифметическом треугольнике» вышла в 1665 году. Она, как следует из названия, была специально посвящена данной таблице и по содержательности опережала своих предшественников.

Открытие в XVI веке алгебраического решения уравнений третьей и четвертой степени являлось не только, без сомнения, большим шагом в развитии алгебры, но и ставило перед наукой новые проблемы. Так, не меньшее значение имела алгебраическая символика, над проблемой создания которой трудились многие математики (см., например, «Знаки равенства и неравенства», «Строгие и нестрогие неравенства»).

Европейские ученые Региомонтан[26], Пачоли, Шюке[27], Видман[28] и др., вводя алгебраические знаки (вторая половина XV века), положили начало алгебраическим счислениям.

Рисунок 10. Региомонта́н (Иоганн Мюллер)

Рисунок 11. Лу́ка Пачо́ли

В XVI веке буквенная символика (см. также «О буквенных коэффициентах») развивается и совершенствуется благодаря трудам немецких, английских, нидерландских и французских математиков.

Остановимся, например, на таком видном немецком математике XVI века, как Михаэль Штифель (см. выше относительно «арифметического треугольника»).

В молодости (в 1511 году) Михаэль, выросший в состоятельной семье и получивший в Виттенбергском университете[29] звание магистра, постригся в монахи и проживал в католическом августинском[30] Эсслингенском монастыре.

Во времена Реформации[31] Михаэль примкнул к движению Лютера[32] и стал сельским пастором[33]. В этот период Михаэль увлекается нумерологией и пытается предсказать дату «конца света»[34] при помощи чисел, встречающихся в Библии. Для нахождения «искомой даты» Штифель заменял числа из Библии словами, буквы которых должны соответствовать «треугольным числам»[35] и т.д. На основе сделанных «исследований» Штифель публично предсказывает дату конца света – 19 октября 1533 года. Это приводит к панике среди его прихожан и других суеверных[36] людей. Многие, веруя в правоту пастора, ликвидируют свои коммерческие предприятия, раздают и уничтожают вещи и деньги. Но после того, как указанная Штифелем дата прошла, обманутая паства набросилась на своего пастора и заключила его в Вюртембергскую тюрьму. Только стараниями самого основателя Реформации – Лютера – Штифель был выпущен на свободу.

Произошедшее сильно повлияло на мировоззрение Михаэлья Штифеля. Он посвящает дальнейшие исследования чистой (без религиозных составляющих) математике и значительно преуспевает в этом направлении.

В 1544 году издана его книга «Arithmetica integra» («Полная арифметика»), а в 1545 году «Немецкая арифметика» («Deutsche Arithmetik»). Примеры сложения положительных и отрицательных чисел из «Арифметики» 1545 года приведены на рисунке 12.

Рисунок 12. Примеры сложения положительных и отрицательных чисел из «Арифметики» М. Штифеля 1545 года.

В 1553 году он издал дополненную им «Алгебру» Кристофа Рудольфа[37] («Косс») – «Алгебру Кристофа Рудольфа с прекрасными примерами алгебры, улучшенную и весьма увеличенную Михаэлем Штифелем».

Будучи самоучкой в области математики Штифель, тем не менее, был в курсе всех математических достижений своего времени. Так, в одно из своих произведений он включает алгебраическое решение уравнений третьей и четвертой степени, найденное итальянскими учеными-математиками. Штифель считается предшественником Джона Непера[38] – изобретателя логарифмов.

Штифель первым рассматривал отрицательные числа, как числа меньше нуля. Он одним из первых вводит знак корня с целым показателем и применяет символы для многих неизвестных.

То, что кажется сейчас обыденностью, а именно – сокращение слов и применение (изобретение) знаков и символов, позволило в значительной мере упростить понимание основ алгебры, как науки.

В 1557 году Роберт Рекорд[39] вводит в употребление знак равенства.

Франсуа Виет[40], будучи юристом и практикующим адвокатом, в 1579 году издает работу «Математические таблицы», а в 1591 году – «Введение в аналитическое искусство», в котором им впервые введены буквенные обозначения для неизвестных и коэффициентов уравнений.

Использование алгебраической символики (взамен словесной), позволило Виету установить единообразный прием решения уравнений, выражая как зависимости между составляющими частями уравнений, так и между их результатами общими формулами.

Символика, вводимая учеными того времени, была далека от употребляемой в настоящее время. В качестве примера приведем одно из уравнений, описываемых в произведении Виета:

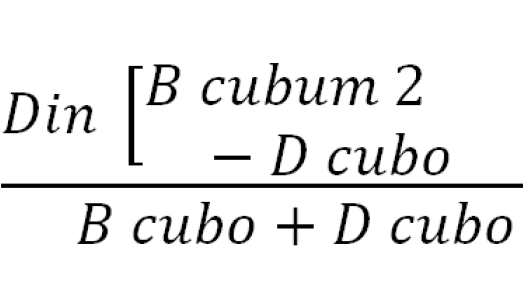
Сравните приведенное выше уравнение с уравнением, написанным с применением современных символов:

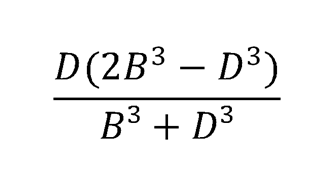
Но стоит только представить эту формулу исключительно в словесном описании, как становится понятной вся революционность вводимых изменений.

В XVII веке совершенствование алгебраической символики продолжено в трудах Гарриота (Хэрриота)[41], Оутреда[42], Ньютона[43] и других ученых.

Понятийная составляющая – базис любой науки. Это то, что позволяет общаться ученым разных стран на одном языке, понимать друг друга без излишних пояснений, исключая, порой сами слова из общения.

Трудно себе представить, но на протяжении XVI – XVII веков ученые для обозначения одного и того же понятия применяли разные знаки, но один и тот же знак, с другой стороны, мог применяться разными математиками в разном смысле.

Например:

• Рекорд обозначал известным нам сейчас знаком «=» равенство, т.е. – равно;
• Виет знак «=» применял как знак вычитания (!!!);
• Декарт пользовался знаком «=» вместо употребляемого нами знака «±».

Другой пример: знак «ꝏ»[44] для Декарта был знаком равенства, а для Джона Валлиса[45] знаком бесконечности.

Представьте, с каким трудом понимали друг друга ученые, претендующие на «пальму первенства» при написании своих книг, трудов и трактатов. И с какими трудностями во взаимопонимании приходилось сталкиваться их ученикам, не допускающим, порой, даже мысли об отклонении от привитых учителем знаний и «формул».

Лишь в XVIII веке повсюду утверждается современная алгебраическая символика.

[1]    «Малым искусством» называли арифметику.

[2]    Боло́нья – город на севере Италии.

[3]    Болонский университет – итальянский государственный университет, старейший университет в мире.

[4]    Фра Лу́ка Бартоломе́о де Пачо́ли (Пачиоли или Пачиоло, 1445 – 19 июня 1517) – итальянский математик, один из основоположников современных принципов бухгалтерии.

[5]    Копе́рник Никола́й (19 февраля 1473 – 24 мая 1543) – польский и немецкий астроном, математик, механик, экономист.

[6]    Сципио́н дель Фе́рро (6 февраля 1465 – 5 ноября 1526) – итальянский математик, открывший общий метод решения неполного кубического уравнения.

[7]    Человек этот не снискал себе какой-либо широкой научной славы кроме той, что некоторое время использовал секрет своего учителя для участия в научных диспутах.

[8]    Тарта́лья Никколо́ (1499 – 1557) – итальянский математик-самоучка, педагог, инженер фортификационных сооружений.

[9]    Бре́шиа (Брешия) – город на севере Италии.

[10] Война Камбрейской лиги – война, продолжавшаяся с 1508 по 1516 год.

[11] Информация предоставлена на основании Энциклопедического словаря Брокгауза и Ефрона.

[12] Архиме́д (287 – 212 годы до н.э.) – древнегреческий ученый и инженер.

[13] Веро́на – город на севере Италии.

[14] Карда́но Джеро́ламо (Джироламо, Иероним, 24 сентября 1501 – 21 сентября) – итальянский математик, инженер, философ, врач, астролог.

[15] Лодовико (Луиджи) Феррари (2 февраля 1522 – 5 октября 1565 года) – итальянский математик.

[16] Книга издана в Венеции в 1556 году.

[17] Ачарья Пингала (ок. III / II вв. до н.э.) – древнеиндийский математик, автор Чандамшастры («Чандас-шастра» или «Чандас-сутра»).

[18] Халаюдха (X век) – индийский математик.

[19] Гия́с-ад-Ди́н Абу-ль-Фатх Ома́р ибн Ибрахи́м Хайя́м Нишапури́ (Ома́р Хайя́м, 18 мая 1048 – 4 декабря 1131) – персидский философ, математик, астроном, поэт.

[20] Чжу Шицзе (кит. 朱世杰), псевдоним Сунтин (кит. 松庭), 1249 – 1314) – один из крупнейших математиков Китая XIII – начала XIV века.

[21] Ян Хуэ́й (кит.трад. 楊輝, упр. 杨辉, пиньинь Yáng Huī), 1238 – 1298) – китайский  математик из группы сунских алгебраистов XIII – XIV веков. Педагог-методолог.

[22] Гияс-ад-дин Джамшид ибн Масуд аль-Каши (1380 – 22 июня 1429) – персидский ученый, один из видных математиков и астрономов XV века.

[23] Петер Апиан (Петер Биневиц или Бенневиц, 16 апреля 1495 – 21 апреля 1552) – немецкий механик и астроном.

[24] Михаэль Штифель (около 1487 – 19 апреля 1567) – немецкий математик, один из изобретателей логарифмов, активный деятель Реформации.

[25] Блез Паска́ль (19 июня 1623 – 19 августа 1662) – французский математик, механик, физик, литератор, философ и теолог.

[26] Региомонта́н (подлинное имя – Иоганн Мюллер, 6 июня 1436 – 6 июля 1476) – немецкий астроном, математик, астролог.

[27] Никола́ Шюке́ (1445(?) – около 1488) – французский математик.

[28] Иоганн Видман (около 1460 – около 1505) – немецкий математик. Получил известность тем, что первым употребил и опубликовал современные плюса и минуса.

[29] Виттенбергский университет – университет в Германии. Был основан в Виттенберге в 1502 году.

[30] Августи́нский о́рден, августинцы – неофициальное наименование членов нескольких монашеских орденов и конгрегаций католической церкви, руководствующихся «Уставом святого Августина».

[31] Реформа́ция – религиозное движение в Западной и Центральной Европе XVI – начала XVII века, на первоначальном этапе направленное на реформирование католической церкви, а на заключительном – на отделение от неё и образование новой христианской конфессии – протестантизма.

[32] Ма́ртин Лю́тер (монашеское имя — Августин, 10 ноября 1483 – 18 февраля 1546) – немецкий христианский богослов, монах-августинец, ведущий переводчик Библии на немецкий язык, инициатор Реформации, именем которого названо одно из его крупнейших направлений – лютеранство.

[33] В лютеранских общинах «пасторами» называют людей, призванных для публичной проповеди и совершения таинств.

[34] Коне́ц све́та – распространённый фразеологизм, означающий реальную либо воображаемую угрозу прекращения существования всех людей и цивилизаций, человечества или даже Земли и Вселенной целиком. В узком смысле – уничтожение всего живого.

[35] Треугольное число – один из классов фигурных многоугольных чисел, определяемый как число точек, которые могут быть расставлены в форме правильного треугольника.

[36] Суеве́рие – предрассудок, восприятие сил и явлений, не находящих себе у воспринимающего обоснования.

[37] Кри́стоф (Христоф) Ру́дольф (1499 – 1545) – немецкий математик, автор первого немецкого учебника алгебры, в котором предложил знак радикала, закрепившийся в науке. Принадлежал к школе «коссистов» (немецких алгебраистов XVI века).

[38] Джон Не́пер (1550 – 1617) – шотландский математик, астроном. Один из изобретателей логарифмов, первый, кто опубликовал логарифмические таблицы.

[39] Роберт Рекорд (около 1510 – 1558) – валлийский врач и математик. Известен, в частности, тем, что в 1557 году предложил использовать в математике знак равенства.

[40] Франсуа́ Вие́т, сеньор де ля Биготьер (1540 – 23 февраля 1603) – французский математик, основоположник символической алгебры.

[41] То́мас Хэ́рриот (Харриот или Гарриот, 1560 – 2 июля 1621) – английский астроном, математик, этнограф, переводчик. Заслужил известность, в том числе, благодаря усовершенствованию алгебраической символики, введя в знаки «>» («больше») и «<» («меньше»).

[42] Уи́льям О́тред (Вильям Отред или Вильям Оутред, 5 марта 1574 – 30 июня 1660) – английский математик. Известен как изобретатель логарифмической линейки (1622 год) и один из создателей современной математической символики.

[43] Исаа́к Нью́то́н (4 января 1643 – 31 марта 1727 по григорианскому календарю) – английский физик, математик, механик, астроном.

[44] Знак, ныне обозначающий «бесконечность».

[45] Джон Ва́ллис (Уо́ллис) (23 ноября 1616 – 28 октября 1703) – английский математик.