Математический юмор

В ответе к задаче №159 был приведен пример:
какое из нижеуказанных выражений больше?

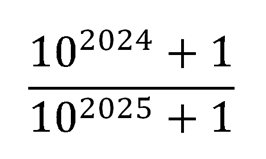
или

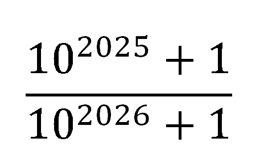
Прежде, чем мы найдем ответ на поставленный вопрос, отвлечемся от этого примера и обратимся к самой математике, как науке. Математика, признаете вы это или нет, не только «сухая наука», а весьма и весьма занятный предмет изучения. Всё зависит от того, насколько вы погружены в математику или, если позволите, насколько вам вообще интересны «точные науки».

Небольшой экскурс в историю.

Представьте себе, что вы живете в Европе XVI века. Человек вы достаточно образованный, в алгебре достаточно разбирающийся, в отличие от тех, кто только постигал азы этой науки (см. Зарождение алгебры), и со знанием дела можете посещать «математические поединки» (см. История алгебры в XVI веке). Умнейшие люди вашего столетия изыскивают перед вами алгебраическое решение уравнений третьей степени. «Битва», можно сказать, «не на жизнь, а на смерть». На кону репутация соревнующихся. Более того, их источники дохода во многом зависят от результатов этой «битвы». Каждый из них старается найти для соперника задачу, которую тот не сможет решить. Увлекательное зрелище, не правда ли?

Или, если вы пожелаете, углубимся еще дальше в историю. Вы в древней Греции. Зенон[1] доказывает вам, что Ахиллес[2] никогда не догонит черепаху (см. Апории Зенона), а софисты[3] развлекают вас тем, что доказывают невозможное: «4=5» или то, что вообще все числа равны между собой (см. «Софизмы»). И все это интересно, увлекательно, с использованием доказательной базы. И многие им верят.

Готовы ли вы поверить в то, что 4=5? Или в то, что быстроногий Ахиллес не сможет догнать тихоходную черепаху? Или сможете доказать обратное? Попробуйте опровергнуть древних греков, если есть немного свободного времени.

Теперь вернемся к вопросу, который был задан в самом начале и попытаемся ответить:
Какое из нижеуказанных выражений больше?

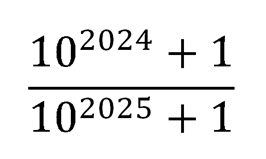
или

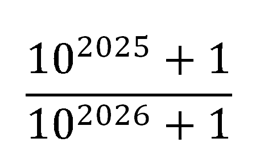
Весь «сухой юмор» математики заключается не столько в том, что нам нет необходимости производить вычисления и сравнивать полученные после вычислений значения, а в том, что при внимательном изучении степеней в числах мы можем заметить закономерность: степени к числу 10 изменяются достаточно незначительно. Более того, в знаменателе первого выражения они равны степени в числителе второго выражения. Это существенно облегчает нам задачу.
Чем?
Заменим

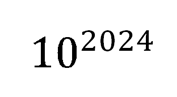
на «с». Получим

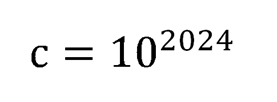
Как вы видите, нам совершенно неважно, в какую степень возведено число 10. Имеет значение приемлемое для поиска ответа отклонение в степенях сравниваемых в выражениях чисел.
Осталось доказать (или опровергнуть) утверждение, что при любом положительном «с»

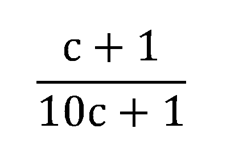
больше, чем

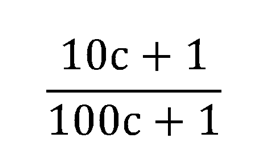
С целью доказательства мы увеличим оба сравниваемые выражения в (10с+1)(100с+1) раз.

Получаем:

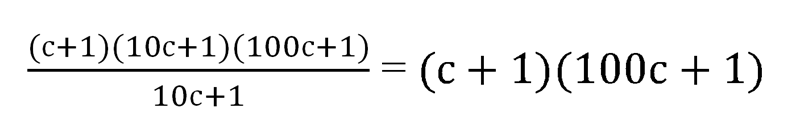
и

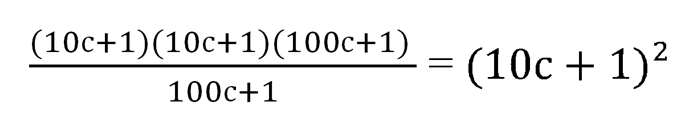
Отсюда

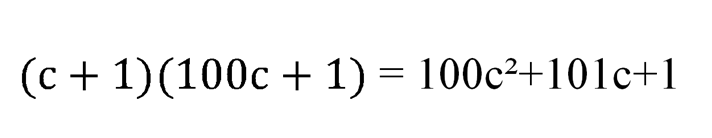
и

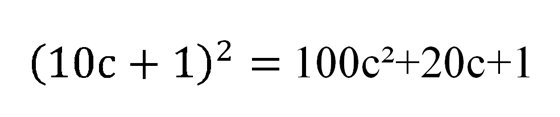
То есть

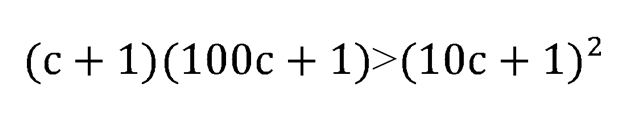
Это означает, что

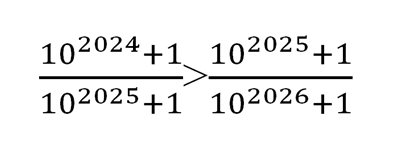
Проверьте, будет ли утверждение верным, если мы заменим 10 на любое другое натуральное положительное число, начиная с двойки.

[1]     Зено́н Эле́йский (около 490 года до н.э. – около 430 года до н.э.) – древнегреческий философ.

[2]     Ахи́лл, или Ахилле́с — персонаж древнегреческой мифологии, один из главных героев «Илиады» Гомера.

[3]     Софисты — древнегреческие платные преподаватели красноречия, представители одноимённого философского направления, распространённого в Греции во 2-й половине V – 1-й половине IV веков до н.э.